Carl David Tolmé Runge (German: [ˈʁʊŋə]; 30 August 1856 – 3 January 1927) was a German mathematician, physicist, and spectroscopist. He was co-developer...
7 KB (534 words) - 09:42, 20 August 2024
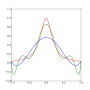
a set of equispaced interpolation points. It was discovered by Carl David Tolmé Runge (1901) when exploring the behavior of errors when using polynomial...
13 KB (1,999 words) - 08:16, 20 August 2024
Science, National Central University. Retrieved 17 April 2022. Runge, Carl David Tolmé (1895), "Über die numerische Auflösung von Differentialgleichungen"...
45 KB (7,387 words) - 09:12, 11 October 2024
Runge–Kutta methods, can be applied to the restated problem and thus be used to evaluate the integral. For instance, the standard fourth-order Runge–Kutta...
22 KB (3,264 words) - 17:45, 24 October 2024
region that includes parts of the imaginary axis, such as the fourth order Runge-Kutta method, is used. This makes the SAT technique an attractive method...
21 KB (3,589 words) - 13:43, 14 October 2024
Hoene-Wroński Joseph Fourier Augustin-Louis Cauchy George Green Carl David Tolmé Runge Martin Kutta Rudolf Lipschitz Ernst Lindelöf Émile Picard Phyllis...
19 KB (3,392 words) - 12:13, 15 October 2024
Hoene-Wroński Joseph Fourier Augustin-Louis Cauchy George Green Carl David Tolmé Runge Martin Kutta Rudolf Lipschitz Ernst Lindelöf Émile Picard Phyllis...
4 KB (435 words) - 14:50, 29 May 2024
l'Académie des Sciences, Série I, 306: 373–376. Courant, Richard; Hilbert, David (1962), Methods of Mathematical Physics, Volume II, Wiley-Interscience....
94 KB (14,079 words) - 09:16, 27 October 2024
Miller(1984) Symmetry and Separation of Variables, Cambridge University Press David Benson (2007) Music: A Mathematical Offering, Cambridge University Press...
19 KB (3,405 words) - 19:42, 10 September 2024
Hoene-Wroński Joseph Fourier Augustin-Louis Cauchy George Green Carl David Tolmé Runge Martin Kutta Rudolf Lipschitz Ernst Lindelöf Émile Picard Phyllis...
9 KB (1,037 words) - 12:04, 30 June 2024
Acoustical Soc of America, 1989; page 18.(retrieved 9 Dec 2012) Speiser, David. Discovering the Principles of Mechanics 1600-1800, p. 191 (Basel: Birkhäuser...
29 KB (3,628 words) - 15:16, 20 August 2024
Hoene-Wroński Joseph Fourier Augustin-Louis Cauchy George Green Carl David Tolmé Runge Martin Kutta Rudolf Lipschitz Ernst Lindelöf Émile Picard Phyllis...
7 KB (1,153 words) - 10:36, 19 March 2023
Peano's second paper pointed out that this footnote was nonsense. Bender, Carl M.; Orszag, Steven A. (1999) [1978], Advanced Mathematical Methods for Scientists...
12 KB (1,450 words) - 17:47, 28 September 2024
second-order method in time. It is implicit in time, can be written as an implicit Runge–Kutta method, and it is numerically stable. The method was developed by...
21 KB (3,803 words) - 17:37, 26 June 2024
investigated by the classical scholars – Laplace, Siméon Denis Poisson, Carl Friedrich Gauss – as a result of which the computations could be performed...
22 KB (2,948 words) - 08:45, 18 October 2024
Hoene-Wroński Joseph Fourier Augustin-Louis Cauchy George Green Carl David Tolmé Runge Martin Kutta Rudolf Lipschitz Ernst Lindelöf Émile Picard Phyllis...
30 KB (4,757 words) - 18:56, 29 September 2024
Hoene-Wroński Joseph Fourier Augustin-Louis Cauchy George Green Carl David Tolmé Runge Martin Kutta Rudolf Lipschitz Ernst Lindelöf Émile Picard Phyllis...
6 KB (993 words) - 21:30, 5 February 2024
differential equations include the Euler–Maruyama method, Milstein method, Runge–Kutta method (SDE), Rosenbrock method, and methods based on different representations...
36 KB (5,616 words) - 15:19, 12 July 2024
numerically integrated using standard techniques such as Euler's method, Runge–Kutta, etc. Finite-difference methods are numerical methods for approximating...
51 KB (7,305 words) - 15:13, 22 October 2024
Trigonometry, Robin Condition, Contemporary Mathematics, 218. 432–437. Logan, J. David, (2001). Transport Modeling in Hydrogeochemical Systems. Springer. J. E...
5 KB (617 words) - 12:18, 22 August 2024
Hoene-Wroński Joseph Fourier Augustin-Louis Cauchy George Green Carl David Tolmé Runge Martin Kutta Rudolf Lipschitz Ernst Lindelöf Émile Picard Phyllis...
17 KB (2,986 words) - 20:53, 15 July 2024
numerical integration using standard techniques such as Euler's method or the Runge-Kutta method. In step (2) above, a global system of equations is generated...
60 KB (7,917 words) - 22:18, 19 October 2024
Hoene-Wroński Joseph Fourier Augustin-Louis Cauchy George Green Carl David Tolmé Runge Martin Kutta Rudolf Lipschitz Ernst Lindelöf Émile Picard Phyllis...
3 KB (541 words) - 16:30, 30 July 2024
Hoene-Wroński Joseph Fourier Augustin-Louis Cauchy George Green Carl David Tolmé Runge Martin Kutta Rudolf Lipschitz Ernst Lindelöf Émile Picard Phyllis...
18 KB (2,123 words) - 04:48, 25 October 2024
Hoene-Wroński Joseph Fourier Augustin-Louis Cauchy George Green Carl David Tolmé Runge Martin Kutta Rudolf Lipschitz Ernst Lindelöf Émile Picard Phyllis...
8 KB (826 words) - 03:40, 5 July 2024
Bence, Cambridge University Press, 2010, ISC_2N 978-0-521-86153-3 Halliday, David; Resnick, Robert (1977), Physics (3rd ed.), New York: Wiley, ISBN 0-471-71716-9...
44 KB (4,890 words) - 01:31, 3 October 2024
Hoene-Wroński Joseph Fourier Augustin-Louis Cauchy George Green Carl David Tolmé Runge Martin Kutta Rudolf Lipschitz Ernst Lindelöf Émile Picard Phyllis...
34 KB (5,651 words) - 14:33, 17 October 2024
Hoene-Wroński Joseph Fourier Augustin-Louis Cauchy George Green Carl David Tolmé Runge Martin Kutta Rudolf Lipschitz Ernst Lindelöf Émile Picard Phyllis...
11 KB (2,621 words) - 12:58, 27 June 2024
Hoene-Wroński Joseph Fourier Augustin-Louis Cauchy George Green Carl David Tolmé Runge Martin Kutta Rudolf Lipschitz Ernst Lindelöf Émile Picard Phyllis...
4 KB (641 words) - 20:46, 9 October 2024
scattering transform Dispersive partial differential equation Logan, J. David (1994). An Introduction to Nonlinear Partial Differential Equations. New...
9 KB (1,085 words) - 17:58, 3 November 2023