In mathematics, the conformal dimension of a metric space X is the infimum of the Hausdorff dimension over the conformal gauge of X, that is, the class...
2 KB (237 words) - 00:49, 12 August 2023
granular, detailed dimension. Dimension tables are not conformed if the attributes are labeled differently or contain different values. Conformed dimensions come...
17 KB (2,568 words) - 16:59, 28 February 2025
In contrast to other types of conformal field theories, two-dimensional conformal field theories have infinite-dimensional symmetry algebras. In some cases...
33 KB (5,674 words) - 01:40, 21 January 2025
infinite-dimensional algebra of local conformal transformations, and conformal field theories can sometimes be exactly solved or classified. Conformal field...
42 KB (7,037 words) - 16:04, 10 July 2025
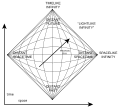
Penrose diagram (redirect from Conformal infinity)
Roger Penrose) is a two-dimensional diagram capturing the causal relations between different points in spacetime through a conformal treatment of infinity...
10 KB (1,198 words) - 15:12, 23 June 2025
in 1850, is a rigidity theorem about conformal mappings in Euclidean space. It states that every smooth conformal mapping on a domain of Rn, where n >...
6 KB (758 words) - 09:00, 10 June 2025
orientation. Conformal maps preserve both angles and the shapes of infinitesimally small figures, but not necessarily their size or curvature. The conformal property...
22 KB (2,515 words) - 03:03, 24 June 2025
conformal geometry is the study of the set of angle-preserving (conformal) transformations on a space. In a real two dimensional space, conformal geometry...
21 KB (3,359 words) - 11:22, 10 January 2025
transformations that preserve the conformal geometry of the space. Several specific conformal groups are particularly important: The conformal orthogonal group. If...
13 KB (1,935 words) - 11:07, 24 June 2025
Virasoro algebra (category Conformal field theory)
central extension of the Witt algebra. It is widely used in two-dimensional conformal field theory and in string theory. It is named after Miguel Ángel...
23 KB (4,140 words) - 21:04, 24 May 2025
In two-dimensional conformal field theory, Virasoro conformal blocks (named after Miguel Ángel Virasoro) are special functions that serve as building blocks...
33 KB (6,417 words) - 05:38, 1 March 2025
A conformal anomaly, scale anomaly, trace anomaly or Weyl anomaly is an anomaly, i.e. a quantum phenomenon that breaks the conformal symmetry of the classical...
12 KB (1,611 words) - 02:51, 14 May 2025
Zee 2010. Conformal field theories are characterized by their invariance under conformal transformations. For an introduction to conformal field theory...
54 KB (6,680 words) - 21:45, 25 May 2025
Liouville field theory (category Conformal field theory)
physics, Liouville field theory (or simply Liouville theory) is a two-dimensional conformal field theory whose classical equation of motion is a generalization...
26 KB (3,921 words) - 15:22, 22 January 2025
definition of one of the core concepts of Kimball's approach to dimensional modeling conformed dimension. The bus matrix defines part of the data warehouse bus...
5 KB (617 words) - 18:12, 16 June 2025
Wess–Zumino–Witten model (redirect from Coset conformal field theory)
also called a Wess–Zumino–Novikov–Witten model, is a type of two-dimensional conformal field theory named after Julius Wess, Bruno Zumino, Sergei Novikov...
21 KB (3,665 words) - 10:25, 19 July 2024
equilibrium critical exponents can be computed from conformal field theory. See also anomalous scaling dimension. Critical exponents also exist for self organized...
19 KB (2,211 words) - 11:09, 15 November 2024
The two-dimensional critical Ising model is the critical limit of the Ising model in two dimensions. It is a two-dimensional conformal field theory whose...
15 KB (3,287 words) - 13:34, 30 August 2024
In conformal geometry, a conformal Killing vector field on a manifold of dimension n with (pseudo) Riemannian metric g {\displaystyle g} (also called...
8 KB (1,308 words) - 14:37, 4 December 2024
Primary field (category Conformal field theory)
of two-dimensional conformal field theory. This terminology is now used both for D=2 and D>2. In d > 2 {\displaystyle d>2} dimensions conformal primary...
9 KB (1,212 words) - 06:33, 1 July 2025
a super conformal field theory the conformal dimension of a chiral multiplet is entirely determined by its R-charge, and so these conformal dimensions...
8 KB (1,006 words) - 10:01, 26 May 2024
W-algebra (category Conformal field theory)
W ( h ) ( z ) {\displaystyle W^{(h)}(z)} is a primary field of conformal dimension h ∈ 1 2 N ∗ {\displaystyle h\in {\frac {1}{2}}\mathbb {N} ^{*}} ...
32 KB (5,488 words) - 01:15, 10 July 2025
Francesco; Pierre Mathieu; David Sénéchal (1997). Conformal field theory. New York: Springer. In the conformal field theory nomenclature, this theory is the...
7 KB (959 words) - 13:32, 9 June 2025
Weyl transformation (category Conformal geometry)
\varphi e^{k\omega }.} Thus conformally weighted quantities belong to certain density bundles; see also conformal dimension. Let A μ {\displaystyle A_{\mu...
3 KB (687 words) - 10:50, 27 March 2025
conformal group. Conformal symmetry encompasses special conformal transformations and dilations. In three spatial plus one time dimensions, conformal...
9 KB (1,120 words) - 21:56, 28 February 2025
James W. Cannon (section 1990s and 2000s: Automatic groups, discrete conformal geometry and Cannon's conjecture)
finite subdivision rules. I. Conformal Geometry and Dynamics, vol. 10 (2006), pp. 63–99. M. Bourdon and H. Pajot, Quasi-conformal geometry and hyperbolic geometry...
23 KB (2,722 words) - 21:26, 21 May 2025
even a conformal map. The plane itself is homeomorphic (and diffeomorphic) to an open disk. For the hyperbolic plane such diffeomorphism is conformal, but...
7 KB (1,672 words) - 16:13, 9 June 2025
Riemann surface (redirect from Conformal invariant)
metrics on X is the additional datum of the conformal structure. A complex structure gives rise to a conformal structure by choosing the standard Euclidean...
26 KB (3,142 words) - 10:43, 20 March 2025
String theory (redirect from 10th dimension)
critical dimension was 10. Stanley Mandelstam formulated a world sheet conformal theory for both the bose and fermi case, giving a two-dimensional field...
122 KB (15,298 words) - 19:57, 8 July 2025
McMullen, Curtis T. (3 October 1997). "Hausdorff dimension and conformal dynamics III: Computation of dimension", Abel.Math.Harvard.edu. Accessed: 27 October...
52 KB (1,139 words) - 22:22, 22 April 2025