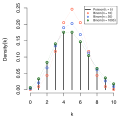
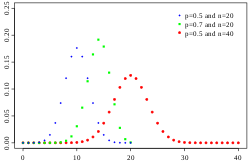
In probability theory, the de Moivre–Laplace theorem, which is a special case of the central limit theorem, states that the normal distribution may be...

limit theorem, a cornerstone of probability theory. Abraham de Moivre was born in Vitry-le-François in Champagne on 26 May 1667. His father, Daniel de Moivre...

of this theorem, that the normal distribution may be used as an approximation to the binomial distribution, is the de Moivre–Laplace theorem. Let { X...

form of a continued fraction; In his theory of probabilities: de Moivre–Laplace theorem that approximates binomial distribution with a normal distribution...

de Moivre's theorem may be: de Moivre's formula, a trigonometric identity Theorem of de Moivre–Laplace, a central limit theorem This disambiguation page...

systems. De Moivre–Laplace theorem In probability theory, the de Moivre–Laplace theorem, which is a special case of the central limit theorem, states that...

holds due to the definition of the exponential function.) De Moivre–Laplace theorem Le Cam's theorem Papoulis, Athanasios; Pillai, S. Unnikrishna. Probability...

considerably less accurate results. This approximation, known as de Moivre–Laplace theorem, is a huge time-saver when undertaking calculations by hand (exact...

We will use a procedure similar to the approximation in de Moivre–Laplace theorem. Contributions from small k i {\displaystyle k_{i}} are of subleading...

limit theorem. Barndorff-Nielson & Cox provide a direct definition of asymptotic normality. Asymptotic analysis Asymptotic theory (statistics) de Moivre–Laplace...

the de Moivre–Laplace theorem (the original, binomial-only version of the central limit theorem) and becomes unreliable when it violates the theorems' premises...

index Davis distribution De Finetti's game De Finetti's theorem DeFries–Fulker regression de Moivre's law De Moivre–Laplace theorem Decision boundary Decision...

Pierre-Simon Laplace de Moivre-Laplace theorem that approximates binomial distribution with a normal distribution Laplace–Bayes estimator Laplace distribution...

binomial's p. According to the central limit theorem (more specifically, the de Moivre–Laplace theorem), the binomial distribution approximates the normal...

for i = 1, 2, ..., ntk may not require any transformation if de Moivre–Laplace theorem is assumed to be at play. Note that if a meta-regression is study-level...

of the central limit theorem Berry–Esséen theorem Berry–Esséen theorem De Moivre–Laplace theorem Lyapunov's central limit theorem Misconceptions about...

theory) Theorem of de Moivre–Laplace (probability theory) Aumann's agreement theorem (statistics) Bapat–Beg theorem (statistics) Basu's theorem (statistics)...

hinted at as early as 1730 by Abraham de Moivre, a pioneering figure in the development of probability theory. De Moivre utilized generating functions to solve...

De Moivre, Abraham (1733), Corollary I – see Walker (1985, p. 77) Stigler (1986, p. 76) Gauss (1809, section 177) Gauss (1809, section 179) Laplace (1774...

proved a special case of the central limit theorem. Sometimes his result is called the theorem of de Moivre–Laplace. A third edition was published posthumously...

{\displaystyle \int _{-\infty }^{\infty }e^{-x^{2}}\,dx={\sqrt {\pi }}.} Abraham de Moivre originally discovered this type of integral in 1733, while Gauss published...

thinks he learned mathematics and probability from a book by Abraham de Moivre. Others speculate he was motivated to rebut David Hume's argument against...

term coefficients. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general linear recurrence problem. George...

the binomial, normal, and chi-squared distributions, as follows. De Moivre and Laplace established that a binomial distribution could be approximated by...

though a related but less precise result was first stated by Abraham de Moivre. One way of stating the approximation involves the logarithm of the factorial:...

subject. Jakob Bernoulli's Ars Conjectandi (posthumous, 1713) and Abraham de Moivre's Doctrine of Chances (1718) treated the subject as a branch of mathematics...

{1}{239}}\right)} The n-th power of a complex number can be computed using de Moivre's formula, which is obtained by repeatedly applying the above formula for...

de Moivre, A. (1738) The doctrine of chances. Woodfall Laplace, P-S (1774). "Mémoire sur la probabilité des causes par les évènements". Mémoires de l'Académie...

limit theorem / (L:R) Berry–Esseen theorem / (F:R) Characteristic function / anl (1F:DCR) De Moivre–Laplace theorem / (L:BD) Helly–Bray theorem / anl...

(1930–2024) Paul-André Meyer (1934–2003) Richard von Mises (1883–1953) Abraham de Moivre (1667–1754) Octav Onicescu (1892–1983) K. R. Parthasarathy (1936–2023)...