In graph theory, the Heawood conjecture or Ringel–Youngs theorem gives a lower bound for the number of colors that are necessary for graph coloring on...

British mathematician Heawood conjecture Heawood graph Heawood number Heywood (surname) This page lists people with the surname Heawood. If an internal link...

the surface of a Klein bottle; this is the only exception to the Heawood conjecture, a generalization of the four color theorem, which would require seven...

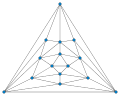
{7+{\sqrt {1+48g}}}{2}}\right\rfloor .} This formula, the Heawood conjecture, was proposed by P. J. Heawood in 1890 and, after contributions by several people...

In mathematics, a conjecture is a conclusion or a proposition that is proffered on a tentative basis without proof. Some conjectures, such as the Riemann...

conjecture Kelvin's conjecture Kouchnirenko's conjecture Mertens conjecture Pólya conjecture, 1919 (1958) Ragsdale conjecture Schoenflies conjecture (disproved...

colleagues. Heawood married in 1890 Christiana Tristram, daughter of Henry Baker Tristram; they had a son and a daughter. Heawood conjecture Heawood number...

in graph theory and contributed significantly to the proof of the Heawood conjecture (now the Ringel–Youngs theorem), a mathematical problem closely linked...

the Heawood number of a surface is an upper bound for the number of colors that suffice to color any graph embedded in the surface. In 1890 Heawood proved...

{\displaystyle K_{3,3,1,1}} are conjectured to generate all excluded minors for 4-flat graphs and μ ≤ 5 {\displaystyle \mu \leq 5} (the Heawood family). Goldberg,...

the Heawood conjecture on the number of colors needed when a two-dimensional surface is partitioned into cells by a graph embedding. The Heawood conjecture...

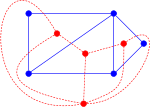
sphere S 2 {\displaystyle S^{2}} A closed disc (with boundary) By the Heawood conjecture, it can be coloured with up to 4 mutually adjacent regions A genus...

problem and the Heawood conjecture on coloring maps on non-planar surfaces such as the torus and Klein bottle. Both had been long-conjectured but were unsolved...

Ringel–Youngs theorem (i.e. Ringel and Youngs's 1968 proof of the Heawood conjecture), which is closely related to the analogue of the four-color theorem...

(now known as "Franklin's system"). In 1934, Franklin disproved the Heawood conjecture for the Klein bottle by showing that any map drawn on the Klein bottle...

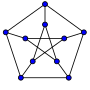
vertex-transitive graphs include the symmetric graphs (such as the Petersen graph, the Heawood graph and the vertices and edges of the Platonic solids). The finite Cayley...

related to the Heawood conjecture by proving that, on any surface other than the sphere or Klein bottle, the only graphs meeting Heawood's bound on the...

Petersen graph, with 10 vertices. The smallest 3-crossing cubic graph is the Heawood graph, with 14 vertices. The smallest 4-crossing cubic graph is the Möbius-Kantor...

constructed from the smaller distance-regular Heawood graph by constructing a vertex for each 6-cycle in the Heawood graph and an edge for each disjoint pair...

omission of some closely related topics, including the proof of the Heawood conjecture on coloring graphs on surfaces by Gerhard Ringel and Ted Youngs. And...

later President of the London Mathematical Society. In 1890, Percy John Heawood pointed out that Kempe's argument was wrong. However, in that paper he...

cubic and symmetric, including the utility graph, the Petersen graph, the Heawood graph, the Möbius–Kantor graph, the Pappus graph, the Desargues graph,...

and others. The study and the generalization of this problem by Tait, Heawood, Ramsey and Hadwiger led to the study of the colorings of the graphs embedded...

as a proof was accepted for eleven years before it was refuted by Percy Heawood. Peter Guthrie Tait gave another incorrect proof in 1880 which was shown...

Steinitz, the geometry of numbers by Minkowski, and map colourings by Tait, Heawood, and Hadwiger. László Fejes Tóth, H.S.M. Coxeter, and Paul Erdős laid the...

includes the 78 graphs of the Heawood family, and it is conjectured that this list is complete. Colin de Verdière (1990) conjectured that any graph with Colin...

theorem, one of the big conjectures in graph theory. While the theorem is true, Kempe's proof is incorrect. Percy John Heawood illustrated it in 1890 with...

with each face of the embedding being a triangle. This embedding has the Heawood graph as its dual graph. The same concept works equally well for non-orientable...

{\displaystyle t} sufficiently larger than s {\displaystyle s} , the above conjecture z ( n , n ; s , t ) = Θ ( n 2 − 1 / s ) {\displaystyle z(n,n;s,t)=\Theta...

James S. Olson and Robert Shadle (Greenwood Publishing, 1996) p68 Edward Heawood, "A History of Geographical Discovery in the Seventeenth and Eighteenth...