of differential geometry and geometric analysis, inverse mean curvature flow (IMCF) is a geometric flow of submanifolds of a Riemannian or pseudo-Riemannian...
8 KB (1,113 words) - 22:57, 11 April 2025
field of differential geometry in mathematics, mean curvature flow is an example of a geometric flow of hypersurfaces in a Riemannian manifold (for example...
12 KB (2,021 words) - 05:29, 1 April 2025
In mathematics, the mean curvature H {\displaystyle H} of a surface S {\displaystyle S} is an extrinsic measure of curvature that comes from differential...
11 KB (1,739 words) - 23:18, 6 April 2025
Gerhard Huisken (section Inverse mean curvature flow)
He is known for foundational contributions to the theory of the mean curvature flow, including Huisken's monotonicity formula, which is named after him...
23 KB (2,224 words) - 03:14, 13 June 2025
Craig Evans as supervisor. Ilmanen and Gerhard Huisken used inverse mean curvature flow to prove the Riemannian Penrose conjecture, which is the fifteenth...
6 KB (584 words) - 11:05, 9 April 2025
inverse mean curvature flow, which they developed. In 1999, Hubert Bray gave the first complete proof of the above inequality using a conformal flow of...
4 KB (527 words) - 19:00, 30 January 2025
mean curvature flow Willmore flow, as in minimax eversions of spheres Inverse mean curvature flow Intrinsic geometric flows are flows on the Riemannian...
4 KB (539 words) - 01:41, 30 September 2024
Richard S. Hamilton (section Mean curvature flow)
curvature tensor.[H95c] Hamilton's theorem, which requires strict convexity, is naturally applicable to certain singularities of mean curvature flow due...
37 KB (3,515 words) - 23:35, 22 June 2025
_{t})\geq 0.} Said otherwise, Hawking mass is increasing for the inverse mean curvature flow. Hawking mass is not necessarily positive. However, it is asymptotic...
4 KB (582 words) - 17:14, 28 May 2025
resistance of an object is a measure of its opposition to the flow of electric current. The inverse quantity is electrical conductance, and is the ease with...
279 KB (31,747 words) - 15:19, 3 July 2025
laminar flow in tubes where D {\displaystyle D} is the internal diameter, μ b {\displaystyle {\mu }_{b}} is the fluid viscosity at the bulk mean temperature...
27 KB (4,502 words) - 13:30, 24 May 2025
Ergodic theory (redirect from Mean ergodic theorem)
study the geodesic flow on Riemannian manifolds, starting with the results of Eberhard Hopf for Riemann surfaces of negative curvature. Markov chains form...
26 KB (3,727 words) - 14:43, 28 April 2025
generalized mean curvature flow equations. J. Differential Geom. 33 (1991), no. 3, 749–786. Huisken, Gerhard; Ilmanen, Tom. The inverse mean curvature flow and...
8 KB (952 words) - 00:18, 19 June 2025
examples of vector flows include the geodesic flow, the Hamiltonian flow, the Ricci flow, the mean curvature flow, and Anosov flows. Flows may also be defined...
14 KB (2,703 words) - 15:52, 29 June 2025
mass. Huisken had earlier initiated the study of volume-preserving mean curvature flow of hypersurfaces of Euclidean space. Huisken and Yau adapted his...
117 KB (10,542 words) - 11:11, 29 May 2025
Airfoil (redirect from Laminar flow airfoil)
the airfoil is an impermeable surface, the flow w ( x ) {\displaystyle w(x)} must balance an inverse flow from V. By the small-angle approximation, V...
29 KB (3,897 words) - 09:35, 4 April 2025
Differential geometry of surfaces (section First and second fundamental forms, the shape operator, and the curvature)
1989. Guilfoyle, B.; Klingenberg, W. (2019). "Higher codimensional mean curvature flow of compact spacelike submanifolds". Trans. Amer. Math. Soc. 372 (9):...
129 KB (17,641 words) - 09:51, 24 June 2025
(also called the principal normal), and r is its instantaneous radius of curvature based upon the osculating circle at time t. These components are called...
251 KB (31,179 words) - 15:17, 3 July 2025
the Hubble flow of the expanding universe. The peculiar velocities of nonrelativistic particles decay as the universe expands, in inverse proportion with...
37 KB (4,571 words) - 05:41, 23 June 2025
_{xx}+2|\varphi |^{2}\varphi =0} . The zero-curvature equation is so named as it corresponds to the curvature being equal to zero if it is defined F μ ν...
24 KB (3,272 words) - 22:49, 6 July 2025
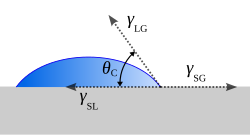
Contact angle (section Contact angle curvature)
liquid-vapor boundary is due to Laplace pressure, which is proportional to the mean curvature. Solving the above equation for both convex and concave surfaces yields:...
31 KB (4,144 words) - 01:11, 11 July 2025
Fluid thread breakup (section Flow from a faucet)
function of the mean curvature of the interface at a given location at the surface, meaning the pressure is dependent on the two radii of curvature that give...
27 KB (4,276 words) - 18:32, 12 May 2024
Spacetime (redirect from Time-space curvature)
the curvature of spacetime. These tidal accelerations are strictly local. It is the cumulative total effect of many local manifestations of curvature that...
132 KB (19,765 words) - 09:00, 3 June 2025
Moscicka-Grzesiak, H. Gruszka and M. Stroinski, ‘‘Influence of Electrode Curvature on Predischarge Phenomena and Electric Strength at 50 Hz of a Vacuum R...
12 KB (1,659 words) - 02:55, 23 May 2025
inverse of Exponential map. Mean curvature Metric ball Metric tensor Minkowski space Minimal surface is a submanifold with (vector of) mean curvature...
28 KB (3,756 words) - 15:15, 3 July 2025
associated Riemann-Hilbert boundary value problem, and then applies mean curvature flow and the Sard–Smale Theorem on regular values of Fredholm operators...
19 KB (2,335 words) - 12:46, 9 July 2025
General relativity (redirect from Spatial curvature)
of space and time, or four-dimensional spacetime. In particular, the curvature of spacetime is directly related to the energy and momentum of whatever...
194 KB (22,694 words) - 15:35, 30 June 2025
tension γ {\displaystyle \gamma } and H f {\displaystyle H_{f}} the mean curvature. This suppresses small-wavelength (high-wavenumber) disturbances, and...
10 KB (1,327 words) - 15:54, 10 July 2025
space-time curvature is evolving lock-step with the others. This presents a mystery: how did these new regions know what temperature and curvature they were...
109 KB (12,924 words) - 00:46, 2 July 2025
four-dimensional spacetime, and the flow of time changes depending on the curvature of spacetime and the spacetime trajectory of the observer. How can these...
104 KB (11,406 words) - 04:05, 21 June 2025