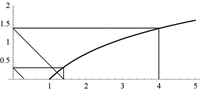
the iterated logarithm of n {\displaystyle n} , written log*  n {\displaystyle n} (usually read "log star"), is the number of times the logarithm function...

the iterated logarithm describes the magnitude of the fluctuations of a random walk. The original statement of the law of the iterated logarithm is due...

series History of logarithms Hyperbolic sector Iterated logarithm Otis King Law of the iterated logarithm Linear form in logarithms Linearithmic List...

include the double logarithm ln(ln(x)), the super- or hyper-4-logarithm (a slight variation of which is called iterated logarithm in computer science)...

Superposition of the previous three graphs Iterated logarithm Napierian logarithm List of logarithmic identities Logarithm of a matrix Logarithmic coordinates...

iterated exponentials, as it is common to call expressions of this form iterated exponentiation, which is ambiguous, as this can either mean iterated...

In mathematics, the Wiener process (or Brownian motion, due to its historical connection with the physical process of the same name) is a real-valued continuous-time...

definition of an iterated function on a set X follows. Let X be a set and f: X → X be a function. Defining f n as the n-th iterate of f, where n is a...

binary logarithm of 1 is 0, the binary logarithm of 2 is 1, the binary logarithm of 4 is 2, and the binary logarithm of 32 is 5. The binary logarithm is the...

Invariance Principle for the Law of the Iterated Logarithm defined a functional form of the law of the iterated logarithm, showing a form of scale invariance...

bounded to O ( log ∗ ⁡ ( n ) ) {\displaystyle O(\log ^{*}(n))} , the iterated logarithm of n {\displaystyle n} , by Hopcroft and Ullman. In 1975, Robert Tarjan...

2005), and every graph whose average degree is exponential in the iterated logarithm of n necessarily contains a cycle whose length is a power of two (Sudakov...

founders of modern probability theory, discovering the law of the iterated logarithm in 1924, achieving important results in the field of limit theorems...

functions Meijer G-function Fox H-function Hyper operators Iterated logarithm Pentation Super-logarithms Tetration Lambert W function: Inverse of f(w) = w exp(w)...

straightened by plotting them using a logarithmic scale for the growth axis. Iterated logarithm – Inverse function to a tower of powers (an even slower growth model)...

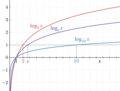
relative error between their logarithms is still large; however, the relative error in their second-iterated logarithms is small: log 10 ⁡ ( log 10 ⁡...

where the number of terms in the sum is bounded above by the binary iterated logarithm. To be precise, let f ( x ) = ⌊ log 2 ⁡ x ⌋ {\displaystyle f(x)=\lfloor...

the form of F. Another result, which follows from the law of the iterated logarithm, is that lim sup n → ∞ n ‖ F ^ n − F ‖ ∞ 2 ln ⁡ ln ⁡ n ≤ 1 2 , a.s...

theorem and a 'concrete' illustration Berry–Esséen theorem Law of the iterated logarithm Random walk Poisson process Compound Poisson process Wiener process...

at most proportional to its logarithm; therefore, the additive persistence is at most proportional to the iterated logarithm, and the smallest number of...

constant approximately equal to 2.71828 that is the base of the natural logarithm and exponential function. It is sometimes called Euler's number, after...

Cajori, Florian (1952) [March 1929]. "§472. The power of a logarithm / §473. Iterated logarithms / §533. John Herschel's notation for inverse functions /...

value } bitreader.close(); intwriter.close(); } Elias omega coding Iterated logarithm "1968 paper by V. I. Levenshtein (in Russian)" (PDF). David Salomon...

primarily useful for functions that grow extremely slowly: (binary) iterated logarithm (log*) is less than 5 for all practical data (265536 bits); (binary)...

deviation principle Law of large numbers (weak/strong) Law of the iterated logarithm Maximal ergodic theorem Sanov's theorem Zero–one laws (Blumenthal...

deviation principle Law of large numbers (weak/strong) Law of the iterated logarithm Maximal ergodic theorem Sanov's theorem Zero–one laws (Blumenthal...

theorem Keynes' Treatise on Probability Law of averages Law of the iterated logarithm Law of truly large numbers Lindy effect Regression toward the mean...

numbers b, in terms of exponential and logarithm function. Specifically, the fact that the natural logarithm ln(x) is the inverse of the exponential...

number is proportional to its logarithm; therefore, the additive persistence is proportional to the iterated logarithm. The example below implements the...

chance of landing on 2. The central limit theorem and the law of the iterated logarithm describe important aspects of the behavior of simple random walks...