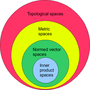
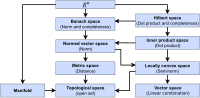
In mathematics, a norm is a function from a real or complex vector space to the non-negative real numbers that behaves in certain ways like the distance...

field of mathematics, norms are defined for elements within a vector space. Specifically, when the vector space comprises matrices, such norms are referred...

In mathematics, the operator norm measures the "size" of certain linear operators by assigning each a real number called its operator norm. Formally,...

speakers frequently refer Norm (mathematics), a map that assigns a length or size to a mathematical object, including: Vector norm, a map that assigns a length...

In mathematical analysis, the uniform norm (or sup norm) assigns, to real- or complex-valued bounded functions ⁠ f {\displaystyle f} ⁠ defined on a set...

In mathematics, a normed vector space or normed space is a vector space over the real or complex numbers on which a norm is defined. A norm is a generalization...

is closely related to the notions of magnitude, distance, and norm in various mathematical and physical contexts. In 1806, Jean-Robert Argand introduced...

In mathematics, a t-norm (also T-norm or, unabbreviated, triangular norm) is a kind of binary operation used in the framework of probabilistic metric...

1 {\displaystyle \ell _{1}} -norm solution is also the sparsest solution". Communications on Pure and Applied Mathematics. 59 (6): 797–829. doi:10.1002/cpa...

media related to Norm Macdonald. Wikiquote has quotations related to Norm Macdonald. Official website (archived) Norm Macdonald at IMDb  Norm Macdonald discography...

In mathematics, specifically functional analysis, the Schatten norm (or Schatten–von-Neumann norm) arises as a generalization of p-integrability similar...

Minkowski functional – Function made from a set Norm (mathematics) – Length in a vector space Seminorm – Mathematical function Superadditivity – Property of a...

In mathematics, in the field of additive combinatorics, a Gowers norm or uniformity norm is a class of norms on functions on a finite group or group-like...

In mathematics, particularly in functional analysis, a seminorm is like a norm but need not be positive definite. Seminorms are intimately connected with...

A social norm is a shared standard of acceptable behavior by a group. Social norms can both be informal understandings that govern the behavior of members...

was the three-dimensional space of Euclidean geometry, but in modern mathematics there are Euclidean spaces of any positive integer dimension n, which...

In mathematics, the magnitude or size of a mathematical object is a property which determines whether the object is larger or smaller than other objects...

In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces. They are...

finite-dimensional p norm spaces Norm (mathematics) – Length in a vector space p {\displaystyle p} -norm – Function spaces generalizing finite-dimensional p norm spacesPages...

In mathematics, the (field) norm is a particular mapping defined in field theory, which maps elements of a larger field into a subfield. Let K be a field...

branch of mathematics, the polarization identity is any one of a family of formulas that express the inner product of two vectors in terms of the norm of a...

functional analysis and related areas of mathematics, a quasinorm is similar to a norm in that it satisfies the norm axioms, except that the triangle inequality...

its magnitude and its direction Magnitude (mathematics), the relative size of an object Norm (mathematics), a term for the size or length of a vector...

cathetus. Mathematics portal Cathetus Triangle Space diagonal Nonhypotenuse number Taxicab geometry Trigonometry Special right triangles Pythagoras Norm...

asymptotic solutions can be blended together using the concept of the Norm (mathematics): N u x = 0.3387 R e x 1 2 P r 1 3 ( 1 + ( 0.0468 P r ) 2 3 ) 1 4...

Minkowski norm may refer to: The proper length in Minkowski space The norm defined in the tangent bundle of a Finsler manifold The vector p-norm The norm defined...

In mathematics, a space is a set (sometimes known as a universe) endowed with a structure defining the relationships among the elements of the set. A...

v by k. A vector space equipped with a norm is called a normed vector space (or normed linear space). The norm is usually defined to be an element of...

In mathematics, a ball is the solid figure bounded by a sphere; it is also called a solid sphere. It may be a closed ball (including the boundary points...

Bounded operators with sub-unit norm Discontinuous linear map Continuous linear operator Local boundedness Norm (mathematics) – Length in a vector space Operator...