In mathematics, a numerical semigroup is a special kind of a semigroup. Its underlying set is the set of all nonnegative integers except a finite number...

the theory of numerical semigroups, the genus of a numerical semigroup is the cardinality of the set of gaps in the numerical semigroup Genus of a quadratic...

mathematics, a semigroup is a nonempty set together with an associative binary operation. A special class of semigroups is a class of semigroups satisfying...

the subset. In this case, it is called a "numerical semigroup". A numerical semigroup is called an Arf semigroup if, for every three elements x, y, and z...

field theory) Artin conductor, of a Galois group Conductor of a Numerical semigroup Conductor (music), a person who leads a musical ensemble Conductor...

19-23). Postage stamp problem Change-making problem Sylver coinage Numerical semigroup The original source is sometimes incorrectly cited as, in which the...

set, and can be described mathematically as the set of gaps of a numerical semigroup. Some of these finite positions, including all of the positions after...

with addition form a monoid, the identity element being 0. Monoids are semigroups with identity. Such algebraic structures occur in several branches of...

gives the non-gaps a numerical semigroup structure, and an old question of Adolf Hurwitz asked for a characterization of the semigroups occurring. A new necessary...

easy to see that this generates a semigroup in some sense—it is not absolutely integrable and so cannot define a semigroup in the above strong sense. Many...

computational algorithms that rely on repeated random sampling to obtain numerical results. The underlying concept is to use randomness to solve problems...

May 1936 – 26 December 2011) was a Scottish mathematician and prominent semigroup theorist. Howie was educated at Robert Gordon's College, Aberdeen, the...

Luca (2013-11-14). "On the variety of linear recurrences and numerical semigroups". Semigroup Forum. 88 (3): 569–574. arXiv:1207.0111. doi:10.1007/s00233-013-9551-2...

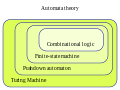
science such as automata theory, syntactic semigroup, model theory and semigroup theory. The class of regular numerical predicate is denoted C l c a {\displaystyle...

abstract algebra, a Moore–Penrose inverse may be defined on a *-regular semigroup. This abstract definition coincides with the one in linear algebra. Drazin...

structures with a single binary operation are: Magma Quasigroup Monoid Semigroup Group Examples involving several operations include: Ring Field Module...

groupoid: S and a single binary operation over S. Semigroup: an associative magma. Monoid: a semigroup with identity element. Group: a monoid with a unary...

defined in this way are continuous semigroups with parameter a {\displaystyle a} , of which the original discrete semigroup of { D n ∣ n ∈ Z } {\displaystyle...

Exponential integrators are a class of numerical methods for the solution of ordinary differential equations, specifically initial value problems. This...

automata transformations or as semigroup homomorphisms, when the state space, S, of the automaton is defined as a semigroup Sg. Monoids are also considered...

, D ) {\displaystyle (\Phi ,D)} : Where Φ {\displaystyle \Phi } is a semigroup, representing combination or aggregation of information, and D {\displaystyle...

more elements of A, with the binary operation of concatenation. The free semigroup A+ is the subsemigroup of A* containing all elements except the empty...

motion of solitons. With Ralph Phillips, Lax developed the Lax-Phillips semigroup in scattering theory, which explained how waves move around obstacles...

The Trotter–Kato theorem can be used for approximation of linear C0-semigroups. By the Baker–Campbell–Hausdorff formula, ( e A / n e B / n ) n = e A...

Journal of Mathematics Russian Mathematical Surveys Scripta Mathematica Semigroup Forum SIAM Journal on Applied Mathematics SIAM Journal on Discrete Mathematics...

abundant in mathematics; in fact, many algebraic structures (such as semigroups and categories) explicitly require their binary operations to be associative...

distributions. For linear equations, one can usually find a mild solution via semigroup techniques. However, problems start to appear when considering non-linear...

Committee for Aeronautics Anne Lester Hudson, American expert in topological semigroups, mathematics educator, and mathematics competition coach Hilda Phoebe...

additional assumptions, be extended to nonlinear systems as well as to semigroup theory, where the crucial advantage of the logarithmic norm is that it...

descriptors are Grassmann operators). Quantum Field Theory Perturbation theory Semigroups Pseudodifferential operators Brownian motion Dilation theory Quantum probability...