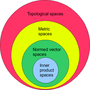
In linear algebra, the quotient of a vector space V {\displaystyle V} by a subspace N {\displaystyle N} is a vector space obtained by "collapsing" N {\displaystyle...

group Quotient space (linear algebra) – Vector space consisting of affine subsets Mapping cone (homological algebra) – Tool in homological algebra Brown...

as spaces. In particular: Quotient space (topology), in case of topological spaces Quotient space (linear algebra), in case of vector spaces Quotient space...

defining quotient objects (also called quotient algebras in universal algebra, and cokernels in category theory). For many types of algebraic structure...

conjugate transpose, and linear operators over a Hilbert space and Hermitian adjoints. However, it may happen that an algebra admits no involution. Look...

and to the quotient space in linear algebra. It is a specific example of a quotient, as viewed from the general setting of universal algebra. Starting...

specifically in linear algebra, a linear subspace or vector subspace is a vector space that is a subset of some larger vector space. A linear subspace is...

In algebra, given a module and a submodule, one can construct their quotient module. This construction, described below, is very similar to that of a...

symmetric algebra over V can be viewed as a "coordinate free" polynomial ring over V. The symmetric algebra S(V) can be built as the quotient of the tensor...

the algebraic dual space. When defined for a topological vector space, there is a subspace of the dual space, corresponding to continuous linear functionals...

In mathematics, the exterior algebra or Grassmann algebra of a vector space V {\displaystyle V} is an associative algebra that contains V , {\displaystyle...

In mathematics, the kernel of a linear map, also known as the null space or nullspace, is the part of the domain which is mapped to the zero vector of...

topological space. A straightforward argument involving elementary linear algebra shows that the only finite-dimensional seminormed spaces are those arising...

In mathematics, a linear algebraic group is a subgroup of the group of invertible n × n {\displaystyle n\times n} matrices (under matrix multiplication)...

{\displaystyle M} is a closed linear subspace of a normed space X , {\displaystyle X,} there is a natural norm on the quotient space X / M , {\displaystyle X/M...

be an affine space, and D be a linear subspace of the associated vector space E → {\displaystyle {\overrightarrow {E}}} . The quotient E/D of E by D...

In mathematics, a Lie algebra (pronounced /liː/ LEE) is a vector space g {\displaystyle {\mathfrak {g}}} together with an operation called the Lie bracket...

concept of vector spaces is fundamental for linear algebra, together with the concept of matrices, which allows computing in vector spaces. This provides...

quotient rings of ring theory, quotient groups of group theory, the quotient spaces of linear algebra and the quotient modules of representation theory...

linear group of a vector space V on the associated projective space P(V). Explicitly, the projective linear group is the quotient group PGL(V) = GL(V) / Z(V)...

mathematics, an algebra over a field (often simply called an algebra) is a vector space equipped with a bilinear product. Thus, an algebra is an algebraic structure...

normed spaces Minkowski distance – Mathematical metric in normed vector space Orthogonal basis Orthogonal complement – Concept in linear algebra Orthonormal...

The cokernel of a linear mapping of vector spaces f : X → Y is the quotient space Y / im(f) of the codomain of f by the image of f. The dimension of the...

specifically in linear algebra, a linear map (also called a linear mapping, linear transformation, vector space homomorphism, or in some contexts linear function)...

structure, the quotient set often inherits a similar structure from its parent set. Examples include quotient spaces in linear algebra, quotient spaces in topology...

A particular case is that of a complex algebra A of continuous linear operators on a complex Hilbert space with two additional properties: A is a topologically...

abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studies modules over these abstract algebraic structures...

mathematics, a Clifford algebra is an algebra generated by a vector space with a quadratic form, and is a unital associative algebra with the additional structure...

variables. Linear algebra is a closely related field that investigates linear equations and combinations of them called systems of linear equations. It...

tensor algebra can be constructed as quotients: these include the exterior algebra, the symmetric algebra, the Clifford algebra, the Weyl algebra, and the...