The Solovay–Strassen primality test, developed by Robert M. Solovay and Volker Strassen in 1977, is a probabilistic primality test to determine if a number...

prime. The Solovay–Strassen test is an Euler probable prime test (see PSW page 1003). For each individual value of a, the Solovay–Strassen test is weaker...

primality test and the Solovay–Strassen primality test. It is of historical significance in the search for a polynomial-time deterministic primality test. Its...

Kanellakis Award for development of 'symbolic model checking,' used in testing computer system designs" (Press release). ACM. 26 Mar 1999. Archived from...

test is not often used in the above form. Instead, other more powerful extensions of the Fermat test, such as Baillie–PSW, Miller–Rabin, and Solovay–Strassen...

the Schönhage–Strassen algorithm. Strassen is also known for his 1977 work with Robert M. Solovay on the Solovay–Strassen primality test, the first method...

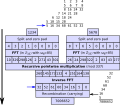
Schönhage–Strassen algorithm is an asymptotically fast multiplication algorithm for large integers, published by Arnold Schönhage and Volker Strassen in 1971...

The AKS primality test (also known as Agrawal–Kayal–Saxena primality test and cyclotomic AKS test) is a deterministic primality-proving algorithm created...

continuum; Outside of set theory, developing (with Volker Strassen) the Solovay–Strassen primality test, used to identify large natural numbers that are prime...

complexity is O(p3). A more efficient multiplication algorithm is the Schönhage–Strassen algorithm, which is based on the Fast Fourier transform. It only requires...

Pépin's test is a primality test, which can be used to determine whether a Fermat number is prime. It is a variant of Proth's test. The test is named...

primality test? More unsolved problems in mathematics The Baillie–PSW primality test is a probabilistic or possibly deterministic primality testing algorithm...

to the probabilistic Solovay–Strassen primality test and the Miller-Rabin test. Inconclusive result: b = 1, in which case the test is inconclusive and...

(1963) is a faster generalization of Karatsuba's method, and the Schönhage–Strassen algorithm (1971) is even faster, for sufficiently large n. The standard...

mathematics, the Lucas–Lehmer–Riesel test is a primality test for numbers of the form N = k · 2n − 1 with odd k < 2n. The test was developed by Hans Riesel and...

Carlo algorithms include the Solovay–Strassen primality test, the Baillie–PSW primality test, the Miller–Rabin primality test, and certain fast variants...

is the sieve's key distinction from using trial division to sequentially test each candidate number for divisibility by each prime. Once all the multiples...

else return false end end end Probable prime Solovay, R.; Strassen, V. (1977-03-01). "A Fast Monte-Carlo Test for Primality". SIAM Journal on Computing....

Lucas–Lehmer Lucas–Lehmer–Riesel Proth's theorem Pépin's Quadratic Frobenius Solovay–Strassen Miller–Rabin Prime-generating Sieve of Atkin Sieve of Eratosthenes...

side of the congruence above, in the manner of trial multiplication. It tests to see if the congruence is satisfied for any value of j {\displaystyle...

Lucas–Lehmer Lucas–Lehmer–Riesel Proth's theorem Pépin's Quadratic Frobenius Solovay–Strassen Miller–Rabin Prime-generating Sieve of Atkin Sieve of Eratosthenes...

methods adapt easily to this application. This can be used for primality testing of large numbers n, for example. Pseudocode A recursive algorithm for ModExp(A...

In computational number theory, the Adleman–Pomerance–Rumely primality test is an algorithm for determining whether a number is prime. Unlike other, more...

Lucas–Lehmer Lucas–Lehmer–Riesel Proth's theorem Pépin's Quadratic Frobenius Solovay–Strassen Miller–Rabin Prime-generating Sieve of Atkin Sieve of Eratosthenes...

Pocklington–Lehmer primality test is a primality test devised by Henry Cabourn Pocklington and Derrick Henry Lehmer. The test uses a partial factorization...

In computational number theory, the Lucas test is a primality test for a natural number n; it requires that the prime factors of n − 1 be already known...

primes (P = 1/2, Solovay–Strassen algorithm). Even when a deterministic primality proof is required, a useful first step is to test for probable primality...

test (QFT) is a probabilistic primality test to determine whether a number is a probable prime. It is named after Ferdinand Georg Frobenius. The test...

reduce computation where those computations would never pass the modulo tests anyway (i.e. would produce even numbers, or multiples of 3 or 5): limit...

Lucas–Lehmer Lucas–Lehmer–Riesel Proth's theorem Pépin's Quadratic Frobenius Solovay–Strassen Miller–Rabin Prime-generating Sieve of Atkin Sieve of Eratosthenes...