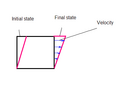
In continuum mechanics, the infinitesimal strain theory is a mathematical approach to the description of the deformation of a solid body in which the...

biological soft tissue. Infinitesimal strain theory, also called small strain theory, small deformation theory, small displacement theory, or small displacement-gradient...

rotations are large enough to invalidate assumptions inherent in infinitesimal strain theory. In this case, the undeformed and deformed configurations of...

infinitesimal strain theory, these conditions are equivalent to stating that the displacements in a body can be obtained by integrating the strains....

mathematics, an infinitesimal number is a non-zero quantity that is closer to 0 than any non-zero real number is. The word infinitesimal comes from a 17th-century...

generalizations of arithmetic operations. Originally called infinitesimal calculus or "the calculus of infinitesimals", it has two major branches, differential calculus...

Elementary Calculus: An Infinitesimal approach is a textbook by H. Jerome Keisler. The subtitle alludes to the infinitesimal numbers of the hyperreal number...

Engineering strain is modeled by infinitesimal strain theory, also called small strain theory, small deformation theory, small displacement theory, or small...

an infinite-sided polygon with infinitesimal sides, and adding the areas of infinitely many triangles with infinitesimal bases. Leibniz used the principle...

be infinitely small, Gottfried Wilhelm Leibniz argued that the theory of infinitesimals implies the introduction of ideal numbers which might be infinitely...

preceding discussion. Bending Bending of plates Infinitesimal strain theory Linear elasticity Plate theory Stress (mechanics) Stress resultants Vibration...

chosen because Leibniz thought of the integral as an infinite sum of infinitesimal summands. The integral symbol is U+222B ∫ INTEGRAL in Unicode and \int...

={\frac {\gamma E}{2(1+\nu )}}} Deformation (mechanics) Infinitesimal strain theory Finite strain theory Pure shear Ogden, R. W. (1984). Non-Linear Elastic...

does not satisfy the Archimedean property. Such fields will contain infinitesimal and infinitely large elements, suitably defined. Suppose F is an ordered...

from the early days of calculus, put on a rigorous footing, such as infinitesimal differences and the derivatives of functions. The term is used in various...

can be shown to have properties that correspond to the properties of infinitesimal and unlimited elements. Nelson's formulation is made more accessible...

Kirchhoff–Love theory φ α = w , α 0 . {\displaystyle \varphi _{\alpha }=w_{,\alpha }^{0}\,.} For the situation where the strains in the plate are infinitesimal and...

Leibniz, uses the symbols dx and dy to represent infinitely small (or infinitesimal) increments of x and y, respectively, just as Δx and Δy represent finite...

mathematician who is given credit for early developments that led to infinitesimal calculus, including his technique of adequality. In particular, he is...

projective line over dual numbers. Smooth infinitesimal analysis Perturbation theory Infinitesimal Screw theory Dual-complex number Laguerre transformations...

around the mid-surface. The original theory developed by Love was valid for infinitesimal strains and rotations. The theory was extended by von Kármán to situations...

including geometry, infinitesimal calculus, trigonometry, algebra, and number theory, as well as continuum physics, lunar theory, and other areas of physics...

online at the Internet Archive. Le Calcul infinitésimal (1823) Leçons sur les applications de calcul infinitésimal; La géométrie (1826–1828) His other works...

specifically on Isaac Newton's notion of fluxions and on Leibniz's notion of infinitesimal change. From his earliest days as a writer, Berkeley had taken up his...

beam theory Deformation (engineering) Finite strain theory Infinitesimal strain theory Moiré pattern Shear modulus Shear stress Shear strength Strain (mechanics)...

 477. ISBN 9780321016188. Alexander, Amir (2015). Infinitesimal: How a Dangerous Mathematical Theory Shaped the Modern World. Great Britain: Oneworld....

extension of the real numbers to include certain classes of infinite and infinitesimal numbers. A hyperreal number x {\displaystyle x} is said to be finite...

that develop within such systems is based on the theory of elasticity and infinitesimal strain theory. When the applied loads cause permanent deformation...

proper class containing not only the real numbers but also infinite and infinitesimal numbers, respectively larger or smaller in absolute value than any positive...

explicit use of indivisibles (indivisibles are geometric versions of infinitesimals). The work was originally thought to be lost, but in 1906 was rediscovered...