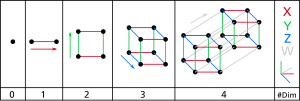mathematics, the Lebesgue covering dimension or topological dimension of a topological space is one of several different ways of defining the dimension of the space...

other is the Lebesgue covering dimension. The term "topological dimension" is ordinarily understood to refer to the Lebesgue covering dimension. For "sufficiently...

descriptions of redirect targets, also called Lebesgue covering dimension if one assumes the axiom of choice see dimension theorem for vector spaces Itzkov, Mikhail...

Lebesgue covering dimension Lebesgue constants Lebesgue's decomposition theorem Lebesgue's density theorem Lebesgue differentiation theorem Lebesgue integration...

topological dimension, also called Lebesgue covering dimension, explains why. This dimension is the greatest integer n such that in every covering of X by...

point. Specifically: A topological space is zero-dimensional with respect to the Lebesgue covering dimension if every open cover of the space has a refinement...

a_{0}=1,\ a_{1}=6} . The sponge's Hausdorff dimension is ⁠log 20/log 3⁠ ≅ 2.727. The Lebesgue covering dimension of the Menger sponge is one, the same as...

the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of higher dimensional Euclidean...

the covering. This definition can be rephrased to make it more similar to that of the Lebesgue covering dimension. The Assouad–Nagata dimension of a...

the dimension as vector space is finite if and only if its Krull dimension is 0. For any normal topological space X, the Lebesgue covering dimension of...

possible to cover, up to a Lebesgue-negligible set, a given subset E of Rd by a disjoint family extracted from a Vitali covering of E. There are two basic...

Four-dimensional space (4D) is the mathematical extension of the concept of three-dimensional space (3D). Three-dimensional space is the simplest possible...

geometry, asymptotic dimension of a metric space is a large-scale analog of Lebesgue covering dimension. The notion of asymptotic dimension was introduced by...

spaces: Complex dimension Hausdorff dimension Inductive dimension Lebesgue covering dimension Packing dimension Isoperimetric dimension Measurements of...

Henri Lebesgue: Blaschke–Lebesgue theorem Cantor–Lebesgue function Borel–Lebesgue theorem Fatou–Lebesgue theorem Lebesgue constant Lebesgue covering dimension...

A five-dimensional space is a space with five dimensions. In mathematics, a sequence of N numbers can represent a location in an N-dimensional space....

Fractional Dimension Julia set Koch snowflake L-system Lebesgue covering dimension Lévy C curve Lévy flight List of fractals by Hausdorff dimension Lorenz...

Lawson topology Polish Space Cantor space Inductive dimension Lebesgue covering dimension Lebesgue's number lemma Polytope Simplex Simplicial complex CW...

In geometry, a three-dimensional space (3D space, 3-space or, rarely, tri-dimensional space) is a mathematical space in which three values (coordinates)...

the real rank of a C*-algebra is a noncommutative analogue of Lebesgue covering dimension. The notion was first introduced by Lawrence G. Brown and Gert...

A two-dimensional space is a mathematical space with two dimensions, meaning points have two degrees of freedom: their locations can be locally described...

In mathematics and specifically in algebraic geometry, the dimension of an algebraic variety may be defined in various equivalent ways. Some of these...

A one-dimensional space (1D space) is a mathematical space in which location can be specified with a single coordinate. An example is the number line...

be understood as a location in n-dimensional space. When n = 7, the set of all such locations is called 7-dimensional space. Often such a space is studied...

}\operatorname {ord} (\beta )} Note that in terms of this definition the Lebesgue covering dimension is defined by dim L e b ⁡ ( X ) = sup α ∈ O D ( α ) {\displaystyle...

original (avi • mp4 • mov • swf • streamed video) on 2011-07-19. "Borel-Lebesgue covering theorem", Encyclopedia of Mathematics, EMS Press, 2001 [1994] Mathworld...

Krull dimension of a commutative ring R, named after Wolfgang Krull, is the supremum of the lengths of all chains of prime ideals. The Krull dimension need...

the Sierpiński carpet is a compact subset of the plane with Lebesgue covering dimension 1, and every subset of the plane with these properties is homeomorphic...

equal to its upper box dimension, which in turn is greater than or equal to the Hausdorff dimension. The Lebesgue covering dimension of a metrizable space...

{\displaystyle A\mapsto \int _{A}f\ \mathrm {d} \lambda ,} with λ the n–dimensional Lebesgue measure. The derivative of this integral at x is defined to be lim...