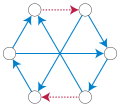
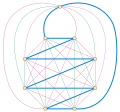
In graph theory, a tournament is a directed graph with exactly one edge between each two vertices, in one of the two possible directions. Equivalently...

In mathematics, and more specifically in graph theory, a directed graph (or digraph) is a graph that is made up of a set of vertices connected by directed...

Appendix:Glossary of graph theory in Wiktionary, the free dictionary. This is a glossary of graph theory. Graph theory is the study of graphs, systems of nodes...

of the Middle Ages Tournament (solitaire), a solitaire card game Tournament (graph theory), a kind of directed graph The Tournament (TV series), a 2005–06...

In graph theory, an orientation of an undirected graph is an assignment of a direction to each edge, turning the initial graph into a directed graph. A...

In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique...

balanced tournament design of order n (a BTD(n)) Tournament (graph theory), mathematical model of a round-robin tournament McMahon system tournament, a variation...

In graph theory, a factor of a graph G is a spanning subgraph, i.e., a subgraph that has the same vertex set as G. A k-factor of a graph is a spanning...

the number theory of quadratic residues, and have interesting properties that make them useful in graph theory more generally. Paley graphs are named after...

the mathematical field of graph theory, a Hamiltonian path (or traceable path) is a path in an undirected or directed graph that visits each vertex exactly...

Pearls in Graph Theory: A Comprehensive Introduction is an undergraduate-level textbook on graph theory by Nora Hartsfield and Gerhard Ringel. It was...

In the mathematical field of graph theory, a graph homomorphism is a mapping between two graphs that respects their structure. More concretely, it is a...

discrete and Euclidean geometries, graph theory, group theory, model theory, number theory, set theory, Ramsey theory, dynamical systems, and partial differential...

A tournament solution is a function that maps an oriented complete graph to a nonempty subset of its vertices. It can informally be thought of as a way...

In the mathematical study of graph theory, a pancyclic graph is a directed graph or undirected graph that contains cycles of all possible lengths from...

specifically in graph theory, a polytree (also called directed tree, oriented tree or singly connected network) is a directed acyclic graph whose underlying...

In the mathematical field of graph theory, the Rado graph, Erdős–Rényi graph, or random graph is a countably infinite graph that can be constructed (with...

Are graphs uniquely determined by their subgraphs? (more unsolved problems in mathematics) Informally, the reconstruction conjecture in graph theory says...

In graph theory and graph algorithms, a feedback arc set or feedback edge set in a directed graph is a subset of the edges of the graph that contains at...

number Berlekamp switching game Salem–Spencer set Secretary problem Tournament (graph theory) Erdős distinct distances problem Leo Moser at the Mathematics...

a universal graph is an infinite graph that contains every finite (or at-most-countable) graph as an induced subgraph. A universal graph of this type...

its graph-theoretic forms, states that one will find monochromatic cliques in any edge labelling (with colours) of a sufficiently large complete graph. To...

In graph theory, the shift graph Gn,k for n , k ∈ N ,   n > 2 k > 0 {\displaystyle n,k\in \mathbb {N} ,\ n>2k>0} is the graph whose vertices correspond...

right. One of the oldest and most accessible parts of combinatorics is graph theory, which by itself has numerous natural connections to other areas. Combinatorics...

areas of spectral graph theory, extremal graph theory and random graphs, in particular in generalizing the Erdős–Rényi model for graphs with general degree...

In graph theory, the Gallai–Hasse–Roy–Vitaver theorem is a form of duality between the colorings of the vertices of a given undirected graph and the orientations...

In graph theory, a branch of mathematics, a Hamiltonian decomposition of a given graph is a partition of the edges of the graph into Hamiltonian cycles...

problems in mathematics) In graph theory, a branch of mathematics, the Erdős–Hajnal conjecture states that families of graphs defined by forbidden induced...

mathematician, who specialized in graph theory. He was widely recognized as one of the "fathers" of modern graph theory. Harary was a master of clear exposition...

types of endorelations include orders, graphs, and equivalences. Specialized studies of order theory and graph theory have developed understanding of endorelations...