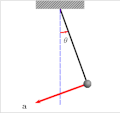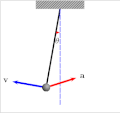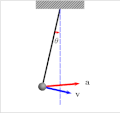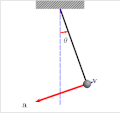
In physics, Lagrangian mechanics is a formulation of classical mechanics founded on the stationary-action principle (also known as the principle of least...

relativistic Lagrangian mechanics is Lagrangian mechanics applied in the context of special relativity and general relativity. The relativistic Lagrangian can...

density Lagrangian (physics), a function in Lagrangian mechanics Lagrangian (field theory), a formalism in classical field theory Lagrangian point, a...

Hamiltonian mechanics is a reformulation of Lagrangian mechanics that emerged in 1833. Introduced by Sir William Rowan Hamilton, Hamiltonian mechanics replaces...

leading to the development of analytical mechanics (which includes Lagrangian mechanics and Hamiltonian mechanics). These advances, made predominantly in...

case one may revert to Newtonian mechanics. Two dominant branches of analytical mechanics are Lagrangian mechanics (using generalized coordinates and...

Lagrangian field theory is a formalism in classical field theory. It is the field-theoretic analogue of Lagrangian mechanics. Lagrangian mechanics is used...

In classical mechanics, Routh's procedure or Routhian mechanics is a hybrid formulation of Lagrangian mechanics and Hamiltonian mechanics developed by...

Hamiltonian constraint Moment map Contact geometry Analysis of flows Nambu mechanics Action (physics) Lagrangian Euler–Lagrange equations Noether's theorem...

Functional derivative Functional integration Hamiltonian mechanics Lagrangian Lagrangian mechanics Measure (physics) Noether's theorem Path integral formulation...

translational symmetry. Advanced formulations of classical mechanics, Lagrangian and Hamiltonian mechanics, allow one to choose coordinate systems that incorporate...

to the conservation of angular momentum throughout the motion. In Lagrangian mechanics, angular momentum for rotation around a given axis, is the conjugate...

T={\tfrac {1}{2}}mv^{2}} and potential V {\displaystyle V} parts of the Lagrangian L = T − V {\displaystyle L=T-V} in arbitrary generalized coordinates the...

of Y → X. In classical mechanics, many dynamical systems are Lagrangian systems. The configuration space of such a Lagrangian system is a fiber bundle...

classical mechanics through quantum mechanics, particle physics, and general relativity. Action principles start with an energy function called a Lagrangian describing...

In celestial mechanics, the Lagrange points (/ləˈɡrɑːndʒ/; also Lagrangian points or libration points) are points of equilibrium for small-mass objects...

Broglie relation is not true in a crystal. Most often in Lagrangian mechanics, the Lagrangian L(q, dq/dt, t) is in configuration space, where q = (q1,...

work–energy principle eliminates the constraint forces underlies Lagrangian mechanics. This section focuses on the work–energy principle as it applies...

T^{*}Q} ; these coordinates are called the canonical coordinates. In Lagrangian mechanics, a different set of coordinates are used, called the generalized...

considering effects of quantization; theories that incorporate quantum mechanics are called quantum field theories. In most contexts, 'classical field...

Displacement field (mechanics) Equivalent latitude Generalized Lagrangian mean Trajectory (fluid mechanics) Liouville's theorem (Hamiltonian) Lagrangian particle...

{H}}\}} denotes the Poisson bracket. Suppose a system is defined by the Lagrangian L with generalized coordinates q. If L has no explicit time dependence...

In mathematics, the inverse problem for Lagrangian mechanics is the problem of determining whether a given system of ordinary differential equations can...

concepts. One of these instances occurs in Lagrangian mechanics. Lagrangian mechanics formulates mechanics in terms of generalized coordinates {qk}, which...

now known as Lagrangian points. Lagrange is best known for transforming Newtonian mechanics into a branch of analysis, Lagrangian mechanics. He presented...

μ {\displaystyle \mu } . Alternatively, a Lagrangian description of the two-body problem gives a Lagrangian of L = 1 2 m 1 r ˙ 1 2 + 1 2 m 2 r ˙ 2 2 −...

derivation of (Eq. 1) Equation 1 can additionally be obtained through Lagrangian Mechanics. More specifically, using the Euler–Lagrange equations (or Lagrange's...

zero-thickness (infinitely thin) string behaviour, using the principles of Lagrangian mechanics. Just as the action for a free point particle is proportional to...

reformulation of the original problem, known as the Lagrangian function or Lagrangian. In the general case, the Lagrangian is defined as L ( x , λ ) ≡ f ( x ) + ⟨...

Semisprays arise naturally as the extremal curves of action integrals in Lagrangian mechanics. Generalizing all these examples, any (possibly nonlinear) connection...