Look up sheaf in Wiktionary, the free dictionary. In mathematics, a sheaf (pl.: sheaves) is a tool for systematically tracking data (such as sets, abelian...
69 KB (11,082 words) - 14:18, 29 June 2025
Look up sheaf in Wiktionary, the free dictionary. Sheaf may refer to: Sheaf (agriculture), a bundle of harvested cereal stems Sheaf (mathematics), a mathematical...
588 bytes (117 words) - 01:39, 23 June 2019
In mathematics, the stalk of a sheaf is a mathematical construction capturing the behaviour of a sheaf around a given point. Sheaves are defined on open...
10 KB (1,588 words) - 01:58, 8 March 2025
Coherent sheaf cohomology is a powerful technique, in particular for studying the sections of a given coherent sheaf. A quasi-coherent sheaf on a ringed...
40 KB (6,934 words) - 00:04, 8 June 2025
Section (redirect from Section (mathematics))
inverse of some morphism Section (fiber bundle), in topology Part of a sheaf (mathematics) Section (group theory), a quotient object of a subobject Conic section...
3 KB (342 words) - 13:22, 1 June 2025
In mathematics, injective sheaves of abelian groups are used to construct the resolutions needed to define sheaf cohomology (and other derived functors...
7 KB (1,059 words) - 05:23, 15 April 2025
Condensed mathematics is a theory developed by Dustin Clausen and Peter Scholze which replaces a topological space by a certain sheaf of sets, in order...
8 KB (811 words) - 16:22, 26 May 2025
Ringed space (redirect from Structure sheaf)
Precisely, it is a topological space equipped with a sheaf of rings called a structure sheaf. It is an abstraction of the concept of the rings of continuous...
9 KB (1,486 words) - 03:46, 4 November 2024
In mathematics, sheaf cohomology is the application of homological algebra to analyze the global sections of a sheaf on a topological space. Broadly speaking...
36 KB (5,833 words) - 23:25, 7 March 2025
(programming language) Processes Ptolemy Project Rust (programming language) Sheaf (mathematics) Threads X10 (programming language) Structured concurrency Operating...
14 KB (1,420 words) - 04:19, 10 April 2025
In mathematics, a constructible sheaf is a sheaf of abelian groups over some topological space X, such that X is the union of a finite number of locally...
6 KB (952 words) - 17:56, 2 July 2025
In mathematics, an invertible sheaf is a sheaf on a ringed space that has an inverse with respect to tensor product of sheaves of modules. It is the equivalent...
3 KB (479 words) - 02:32, 3 March 2025
10. Berlin: Springer Verlag. Tennison, Barry R. (1975), Sheaf theory, London Mathematical Society Lecture Note Series, vol. 20, Cambridge University...
71 KB (7,692 words) - 16:40, 4 July 2025
In mathematics, the constant sheaf on a topological space X {\displaystyle X} associated to a set A {\displaystyle A} is a sheaf of sets on X {\displaystyle...
6 KB (1,008 words) - 14:38, 26 May 2025
In algebraic geometry and other areas of mathematics, an ideal sheaf (or sheaf of ideals) is the global analogue of an ideal in a ring. The ideal sheaves...
4 KB (569 words) - 15:11, 25 April 2025
Algebraic analysis (category Sheaf theory)
Algebraic analysis is an area of mathematics that deals with systems of linear partial differential equations by using sheaf theory and complex analysis to...
4 KB (374 words) - 03:52, 29 March 2025
described using sheaf complexes that are actually perverse sheaves. It was clear from the outset that perverse sheaves are fundamental mathematical objects at...
19 KB (2,265 words) - 05:36, 25 June 2025
topology. Topoi also display deep connections to mathematical logic. Every Grothendieck topos has a special sheaf called a subobject classifier. This subobject...
69 KB (9,328 words) - 07:59, 25 June 2025
The history of mathematics deals with the origin of discoveries in mathematics and the mathematical methods and notation of the past. Before the modern...
148 KB (17,050 words) - 18:16, 8 July 2025
In mathematics, a torsion sheaf is a sheaf of abelian groups F {\displaystyle {\mathcal {F}}} on a site for which, for every object U, the space of sections...
1 KB (131 words) - 17:48, 26 January 2023
Gluing axiom (redirect from B-sheaf)
In mathematics, the gluing axiom is introduced to define what a sheaf F {\displaystyle {\mathcal {F}}} on a topological space X {\displaystyle X} must...
11 KB (1,843 words) - 19:03, 22 June 2025
Topos (redirect from Topos (mathematics))
Francis (1994). Handbook of Categorical Algebra: Volume 3, Sheaf Theory. Encyclopedia of Mathematics and its Applications. Vol. 52. Cambridge University Press...
32 KB (4,308 words) - 19:57, 5 July 2025
ring to be principal Scheme (mathematics) Section conjecture Semistable abelian variety Sheaf cohomology Stack (mathematics) Standard conjectures on algebraic...
82 KB (8,602 words) - 10:27, 8 July 2025
quasi-coherent sheaf on a scheme X means an OX-module that is the sheaf associated to a module on each affine open subset of X. Finally, a coherent sheaf (on a...
44 KB (7,139 words) - 07:51, 25 June 2025
. If X {\displaystyle X} is a scheme over S {\displaystyle S} then the sheaf O X / S {\displaystyle O_{X/S}} is defined by O X / S ( T ) {\displaystyle...
7 KB (844 words) - 13:50, 22 December 2022
In mathematics, the exponential sheaf sequence is a fundamental short exact sequence of sheaves used in complex geometry. Let M be a complex manifold,...
3 KB (485 words) - 15:07, 22 June 2020
In mathematics, a ring is an algebraic structure consisting of a set with two binary operations called addition and multiplication, which obey the same...
99 KB (13,642 words) - 07:01, 14 July 2025
In mathematics, especially in algebraic geometry and the theory of complex manifolds, coherent sheaf cohomology is a technique for producing functions...
26 KB (4,664 words) - 11:28, 9 October 2024
In algebraic geometry, the dualizing sheaf on a proper scheme X of dimension n over a field k is a coherent sheaf ω X {\displaystyle \omega _{X}} together...
7 KB (1,018 words) - 22:42, 28 June 2025
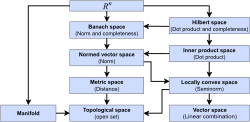
Differentiable manifold (redirect from Sheaf of smooth functions)
charts and atlases). Third, the sheaf OM is not manifestly a sheaf of functions at all. Rather, it emerges as a sheaf of functions as a consequence of...
67 KB (9,497 words) - 20:48, 13 December 2024