mathematics, the Fourier sine and cosine transforms are integral equations that decompose arbitrary functions into a sum of sine waves representing the...

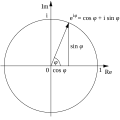
In mathematics, sine and cosine are trigonometric functions of an angle. The sine and cosine of an acute angle are defined in the context of a right triangle:...

"Symmetric convolution and the discrete sine and cosine transforms," IEEE Trans. Signal Process. SP-42, 1038–1051 (1994). Matteo Frigo and Steven G. Johnson:...

respective sine and cosine transforms can be added to express the function. The Fourier transform can be expressed as the cosine transform minus -1 {\displaystyle...

transforms are the discrete sine transform (DST), which is equivalent to a DFT of real and odd functions, and the modified discrete cosine transform (MDCT)...

discrete cosine and sine transforms. H. S. Malvar, "Lapped Transforms for Efficient Transform/Subband Coding", IEEE Trans. on Acoustics, Speech, and Signal...

Fourier introduced sine and cosine transforms (which correspond to the imaginary and real components of the modern Fourier transform) in his study of heat...

/4)={\sqrt {2}}\cos(t-\pi /4)\,,} is the cosine-and-sine (cas) or Hartley kernel. In engineering terms, this transform takes a signal (function) from the time-domain...

example of a trigonometric series. By expressing a function as a sum of sines and cosines, many problems involving the function become easier to analyze because...

wave, a mathematical function Sine and cosine transforms Sine quadrant Sine-Gordon equation Sinë, village in Albania Sine, Washington, a community in the...

list of transforms in mathematics. Abel transform Aboodh transform Bateman transform Fourier transform Short-time Fourier transform Gabor transform Hankel...

and cos and sin are the trigonometric functions cosine and sine respectively. This complex exponential function is sometimes denoted cis x ("cosine plus...

sine wave of arbitrary phase can be written as the linear combination of two sine waves with phases of zero and a quarter cycle, the sine and cosine components...

Fourier transform Fourier operator Fourier inversion theorem Sine and cosine transforms Parseval's theorem Paley–Wiener theorem Projection-slice theorem...

Fourier's sine and cosine transforms also perform even–odd decomposition by representing a function's odd part with sine waves (an odd function) and the function's...

context of a family of discrete cosine transforms, or as DCT-II. More recent standards have used integer-based transforms that have similar properties to...

of its similarity to a raised-cosine distribution. This function is a member of both the cosine-sum and power-of-sine families. Unlike the Hamming window...

interval, [−1,+1], and maps them to two normally distributed samples without the use of sine or cosine functions. The Box–Muller transform was developed as...

1145/317275.317284. Knockaert, Luc (2000). "Fast Hankel transform by fast sine and cosine transforms: the Mellin connection". IEEE Trans. Signal Process....

trigonometry, the law of cosines (also known as the cosine formula or cosine rule) relates the lengths of the sides of a triangle to the cosine of one of its angles...

Specifically, they are the inverses of the sine, cosine, tangent, cotangent, secant, and cosecant functions, and are used to obtain an angle from any of...

so-called integral transforms. In this case, if we make a very large matrix with complex exponentials in the rows (i.e., cosine real parts and sine imaginary parts)...

across the frequency domain of a Fourier transform. Since sine and cosine transforms are related transforms a modified version of the convolution theorem...

not sine and cosine, but sine and versine. A quick, but inaccurate, algorithm for calculating a table of N approximations sn for sin(2πn/N) and cn for...

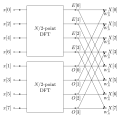
overlap–add and overlap–save methods), fast algorithms for discrete cosine or sine transforms (e.g. fast DCT used for JPEG and MPEG/MP3 encoding and decoding)...

represented as an integral of sines and cosines through the Fourier transform. This has applications to quantum mechanics and communications, among other...

{x}{2}}\right|\,dx:} In the range 0 < φ < 2 π {\displaystyle 0<\varphi <2\pi \,} the sine function inside the absolute value sign remains strictly positive, so the...

frequency). The sines and cosines in the Fourier series are an example of an orthonormal basis. As an example of an application of integral transforms, consider...

A sine function is created by computing the Discrete Hilbert transform of a cosine function, which was processed in four overlapping segments, and pieced...

non-zero integers. The local maxima and minima of the unnormalized sinc correspond to its intersections with the cosine function. That is, ⁠sin(ξ)/ξ⁠ = cos(ξ)...