A Pythagorean triple consists of three positive integers a, b, and c, such that a2 + b2 = c2. Such a triple is commonly written (a, b, c), a well-known...

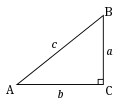
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle...

formulas for generating Pythagorean triples have been developed. Euclid's, Pythagoras' and Plato's formulas for calculating triples have been described here:...

Boolean Pythagorean triples problem is a problem from Ramsey theory about whether the positive integers can be colored red and blue so that no Pythagorean triples...

primitive Pythagorean triples is a mathematical tree in which each node represents a primitive Pythagorean triple and each primitive Pythagorean triple is represented...

equation of degree two that has been studied. Its solutions are the Pythagorean triples. This is also the homogeneous equation of the unit circle. In this...

{\displaystyle y} , and z {\displaystyle z} ; these solutions are known as Pythagorean triples (with the simplest example being 3, 4, 5). Around 1637, Fermat wrote...

Pythagoreanism originated in the 6th century BC, based on and around the teachings and beliefs held by Pythagoras and his followers, the Pythagoreans...

of the Pythagorean theorem, both in the case of an isosceles right triangle and in the general case, as well as lists of Pythagorean triples. In Baudhayana...

the Pythagorean theorem, but that "there is no evidence that they used it to construct right angles". The following are all the Pythagorean triple ratios...

\theta } is a positive integer, as it is with some Pythagorean triangles. For a primitive Pythagorean triple, a2 + b2 = c2, with positive integers a < b <...

relates to a Pythagorean triple, that is, a triple of integers ( s , ℓ , d ) {\displaystyle (s,\ell ,d)} that satisfies the Pythagorean theorem, s 2 +...

vegetarianism before the nineteenth century Pythagorean theorem Pythagorean triple Pythagorean prime Pythagorean trigonometric identity Table of Pythagoras...

transforms a Pythagorean triple into another Pythagorean triple, only one of the two cases is sufficient for producing all primitive Pythagorean triples up to...

integers, the triangle is called a Pythagorean triangle and its side lengths are collectively known as a Pythagorean triple. The relations between the sides...

zero (thus allowing Pythagorean triples to be included) with the only condition being that d > 0. In this setting, a Pythagorean quadruple (a, b, c, d)...

b, c (necessarily satisfying the Pythagorean theorem a2 + b2 = c2), then (a,b,c) is known as a Pythagorean triple. As Martin (1875) describes, the Pell...

value stated. Also, if m and x are rational, so are d, a, b and c. A Pythagorean triple can therefore be obtained from a, b and c by multiplying each of them...

simple Pythagorean triples, such as: (3, 4, 5), (5, 12, 13), (8, 15, 17), (7, 24, 25), and (12, 35, 37), as well as a statement of the Pythagorean theorem...

Similar to a Pythagorean triple, an Eisenstein triple (named after Gotthold Eisenstein) is a set of integers which are the lengths of the sides of a triangle...

{1}{2}}(\eta +\theta )\,.} Furthermore, using double-angle formulae and the Pythagorean identity 1 + tan 2 ⁡ α = 1 / cos 2 ⁡ α {\textstyle 1+\tan ^{2}\alpha...

squares, counted by the sum of squares function; for instance, every Pythagorean triple a 2 + b 2 = c 2 {\displaystyle a^{2}+b^{2}=c^{2}} gives a second representation...

tiling is 13, based on the Pythagorean triple (5,12,13). By overlaying a square grid of side length c onto the Pythagorean tiling, it may be used to generate...

{\displaystyle b^{2}+b^{2}=a^{2}} Here, (b, b, a) is a primitive Pythagorean triple, and from the lemma a is never even. However, this contradicts the...

t2, 1 + t2) values in the above formulae are proportional to the Pythagorean triple (2pq, q2 − p2, q2 + p2). For example, for n = 3 terms, π 2 = arctan...

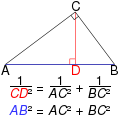
In geometry, the inverse Pythagorean theorem (also known as the reciprocal Pythagorean theorem or the upside down Pythagorean theorem) is as follows: Let...

smallest integer-sided right triangle, making part of the smallest Pythagorean triple (3, 4, 5). 5 is the first safe prime and the first good prime. 11...

taken away. 314: Is an even number Is a squarefree semiprime Forms a Pythagorean triple with 170 and 264 314 (disambiguation) "Sloane's A006881 : Squarefree...

expression of the Pythagorean Theorem in the world, although it had already been known to the Old Babylonians." They make use of Pythagorean triples, which are...

In mathematics, Pythagorean addition is a binary operation on the real numbers that computes the length of the hypotenuse of a right triangle, given its...