versions of Taylor's theorem, some giving explicit estimates of the approximation error of the function by its Taylor polynomial. Taylor's theorem is named...

denoted by the function Rn(x). Taylor's theorem can be used to obtain a bound on the size of the remainder. In general, Taylor series need not be convergent...

Wiles and Richard Taylor proved the modularity theorem for semistable elliptic curves, which was enough to imply Fermat's Last Theorem. Later, a series...

several results in mathematical analysis. Taylor's most famous developments are Taylor's theorem and the Taylor series, essential in the infinitesimal approach...

D = d d x {\displaystyle D={d \over dx}} is an operator version of Taylor's theorem — and is therefore only valid under caveats about f being an analytic...

Rolle's theorem is used to prove the mean value theorem, of which Rolle's theorem is indeed a special case. It is also the basis for the proof of Taylor's theorem...

value theorem Differential equation Differential operator Newton's method Taylor's theorem L'Hôpital's rule General Leibniz rule Mean value theorem Logarithmic...

mathematical analysis, the Whitney extension theorem is a partial converse to Taylor's theorem. Roughly speaking, the theorem asserts that if A is a closed subset...

The fundamental theorem of calculus is a theorem that links the concept of differentiating a function (calculating its slopes, or rate of change at each...

the infinitely small quantities he used. He was the first to prove Taylor's theorem rigorously, establishing his well-known form of the remainder. He wrote...

Taylor's of Loughborough, or Taylor's, in England Taylor Company, a maker of foodservice equipment owned by Middleby Corporation Taylor's theorem, in...

In vector calculus, Green's theorem relates a line integral around a simple closed curve C to a double integral over the plane region D (surface in R...

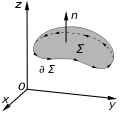
Stokes' theorem, also known as the Kelvin–Stokes theorem after Lord Kelvin and George Stokes, the fundamental theorem for curls or simply the curl theorem, is...

this case, they are also called indefinite integrals. The fundamental theorem of calculus relates definite integration to differentiation and provides...

In vector calculus, the divergence theorem, also known as Gauss's theorem or Ostrogradsky's theorem, is a theorem relating the flux of a vector field through...

distributed. The characteristic function of Y 1 {\textstyle Y_{1}} is, by Taylor's theorem, φ Y 1 ( t n ) = 1 − t 2 2 n + o ( t 2 n ) , ( t n ) → 0 {\displaystyle...

formulas. Taylor's theorem gives a precise bound on how good the approximation is. If f is a polynomial of degree less than or equal to d, then the Taylor polynomial...

In multivariable calculus, the implicit function theorem is a tool that allows relations to be converted to functions of several real variables. It does...

counterclockwise circle of radius r around z, and 0 < r < 1 − |z|. By Taylor's theorem, for each z in the unit disk, there exists 0 ≤ t ≤ 1 such that f(z)...

Noether's theorem states that every continuous symmetry of the action of a physical system with conservative forces has a corresponding conservation law...

mathematics, specifically differential calculus, the inverse function theorem gives a sufficient condition for a function to be invertible in a neighborhood...

In fluid mechanics, the Taylor–Proudman theorem (after Geoffrey Ingram Taylor and Joseph Proudman) states that when a solid body[clarification needed]...

In topology, the Tietze extension theorem (also known as the Tietze–Urysohn–Brouwer extension theorem or Urysohn-Brouwer lemma) states that any real-valued...

generalized Stokes theorem (sometimes with apostrophe as Stokes' theorem or Stokes's theorem), also called the Stokes–Cartan theorem, is a statement about...

The Lange model (or Lange–Lerner theorem) is a neoclassical economic model for a hypothetical socialist economy based on public ownership of the means...

a neighborhood U of the point x 0 {\displaystyle x_{0}} . Then by Taylor's theorem, f ( x ) = f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) + ⋯ + f ( k ) ( x 0...

Solenoidal vector field Stokes' theorem Submersion Surface integral Symmetry of second derivatives Taylor's theorem Total derivative Vector field Vector...

_{k}} guarantee that f {\displaystyle \displaystyle f} is reduced, by Taylor's theorem. Using this definition, the negative of a non-zero gradient is always...

Taylor's theorem that falls between the limits a and b A number used in error approximations for formulas that are applications of Taylor's theorem,...

In physics and mathematics, the Helmholtz decomposition theorem or the fundamental theorem of vector calculus states that certain differentiable vector...