physics, the algebra of physical space (APS) is the use of the Clifford or geometric algebra Cl3,0(R) of the three-dimensional Euclidean space as a model...
11 KB (1,560 words) - 06:44, 17 January 2025
while Dirac algebra uses complex number scalars. The STA spacetime split is similar to the algebra of physical space (APS, Pauli algebra) approach. APS...
48 KB (7,325 words) - 10:33, 9 April 2025
introduced. In geometric algebra (GA) these are multivectors, which sometimes follow Ricci calculus. In the Algebra of physical space (APS), also known as...
42 KB (6,726 words) - 06:28, 14 April 2025
Four-vector (category Theory of relativity)
idea of using the Pauli matrices as basis vectors is employed in the algebra of physical space, an example of a Clifford algebra. In spacetime algebra, another...
47 KB (8,365 words) - 14:48, 25 February 2025
Clifford algebra is an algebra generated by a vector space with a quadratic form, and is a unital associative algebra with the additional structure of a distinguished...
64 KB (9,191 words) - 23:47, 24 April 2025
Dirac equation (section The algebra of physical space)
The Dirac equation in the algebra of physical space uses a Clifford algebra over the real numbers, a type of geometric algebra. As mentioned above, the...
79 KB (13,057 words) - 05:19, 23 April 2025
and in that context goes by the name Algebra of physical space (not to be confused with the Spacetime algebra, which is 16-dimensional.) H.S.M. Coxeter:...
7 KB (718 words) - 06:36, 10 October 2024
geometric algebras applied in physics include the spacetime algebra (and the less common algebra of physical space). Geometric calculus, an extension of GA that...
93 KB (13,801 words) - 22:00, 13 April 2025
variety of different formulations of the algebra to be given, as noted in the examples below. Poisson algebras occur in various settings. The space of real-valued...
6 KB (820 words) - 11:59, 4 October 2024
Bicomplex number (redirect from Fundamental theorem of tessarine algebra)
of CAPS (complexified algebra of physical space), which is Clifford algebra C l ( 3 , C ) {\displaystyle Cl(3,\mathbb {C} )} . Since the linear space...
14 KB (1,806 words) - 21:01, 14 April 2025
analysis, a branch of mathematics, an operator algebra is an algebra of continuous linear operators on a topological vector space, with the multiplication...
5 KB (545 words) - 13:58, 27 September 2024
linear algebra and numerical solution of partial differential equations Stochastic methods, such as Monte Carlo methods and other representations of uncertainty...
6 KB (568 words) - 07:04, 19 March 2025
Discrete mathematics (redirect from History of discrete mathematics)
K[x]_{(x-c)}} of the local ring at (x-c), a point together with a neighborhood around it. Algebraic varieties also have a well-defined notion of tangent space called...
26 KB (2,771 words) - 02:35, 23 December 2024
Spinor (section Exterior algebra construction)
as elements of a vector space that carries a linear representation of the Clifford algebra. The Clifford algebra is an associative algebra that can be...
72 KB (9,924 words) - 12:09, 23 April 2025
Hausdorff space. C*-algebras were first considered primarily for their use in quantum mechanics to model algebras of physical observables. This line of research...
20 KB (2,830 words) - 09:30, 14 January 2025
Pauli matrices (redirect from Pauli algebra)
different Cartan pair gives a similar "X–Y decomposition of a single-qubit gate. Algebra of physical space Spinors in three dimensions Gamma matrices § Dirac...
45 KB (7,495 words) - 07:41, 22 April 2025
Probability theory (redirect from Foundations of the Theory of Probability)
theory to define the probability space: Given any set Ω {\displaystyle \Omega \,} (also called sample space) and a σ-algebra F {\displaystyle {\mathcal {F}}\...
26 KB (3,602 words) - 11:44, 23 April 2025
examples of nontrivial physical phenomena he believes arose from the mathematical tools employed and not from the intrinsic properties of physical reality...
19 KB (2,165 words) - 03:01, 14 April 2025
Vector calculus (redirect from Calculus of vectors)
being defined for a vector space and then applied pointwise to a vector field. The basic algebraic operations consist of: Also commonly used are the...
22 KB (2,135 words) - 04:00, 8 April 2025
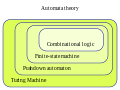
Automata theory (redirect from Theory of automata)
equivalence of deterministic and nondeterministic finite automata. In the 1960s, a body of algebraic results known as "structure theory" or "algebraic decomposition...
32 KB (3,851 words) - 14:40, 16 April 2025
Four-velocity (section Theory of relativity)
counterpart of velocity, which is a three-dimensional vector in space. Physical events correspond to mathematical points in time and space, the set of all of them...
10 KB (1,711 words) - 01:50, 24 November 2024
In mathematics, a Lie algebra (pronounced /liː/ LEE) is a vector space g {\displaystyle {\mathfrak {g}}} together with an operation called the Lie bracket...
61 KB (10,477 words) - 22:23, 2 April 2025
Mathematical software (redirect from Lists of mathematical software)
library, where emphasis is placed on clear understanding of algorithms. Many computer algebra systems (listed above) can also be used for numerical computations...
9 KB (674 words) - 11:16, 23 April 2025
Quaternion (redirect from Methods of quaternions)
Hamilton in 1843 and applied to mechanics in three-dimensional space. The algebra of quaternions is often denoted by H (for Hamilton), or in blackboard...
96 KB (12,648 words) - 18:54, 10 April 2025
Nilpotent (category Algebraic properties of elements)
field of a plane wave without sources is nilpotent when it is expressed in terms of the algebra of physical space. More generally, the technique of microadditivity...
8 KB (1,210 words) - 23:02, 6 March 2025
equation Laws of science Defining equation (physical chemistry) List of equations in classical mechanics Table of thermodynamic equations List of equations...
5 KB (103 words) - 09:21, 8 August 2024
Source, a synchrotron X-ray source at Argonne National Laboratory Algebra of physical space, in physics Ammonium persulfate, in chemistry Apus, abbreviation...
4 KB (523 words) - 12:11, 13 February 2025
Stochastic calculus (category Definitions of mathematical integration)
Bachelier in 1900 and by Albert Einstein in 1905 and other physical diffusion processes in space of particles subject to random forces. Since the 1970s, the...
6 KB (775 words) - 04:24, 10 March 2025
Applied mathematics (redirect from Applications of mathematics)
areas of science (computational science) as well as the mathematics of computation (for example, theoretical computer science, computer algebra, numerical...
23 KB (2,439 words) - 22:28, 24 March 2025
supersymmetry algebra (or SUSY algebra) is a mathematical formalism for describing the relation between bosons and fermions. The supersymmetry algebra contains...
5 KB (726 words) - 18:54, 26 January 2024