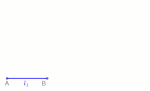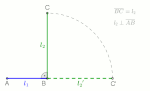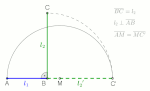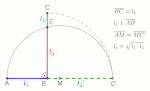
geometric series is a series in which the ratio of successive adjacent terms is constant. In other words, the sum of consecutive terms of a geometric...

the initial value. The sum of a geometric progression's terms is called a geometric series. The nth term of a geometric sequence with initial value a =...

arithmetico-geometric series is a sum of terms that are the elements of an arithmetico-geometric sequence. Arithmetico-geometric sequences and series arise in various...

}}x^{n}.} The Taylor series of any polynomial is the polynomial itself. The Maclaurin series of ⁠1/1 − x⁠ is the geometric series 1 + x + x 2 + x 3 + ⋯...

In mathematics, an infinite geometric series of the form ∑ n = 1 ∞ a r n − 1 = a + a r + a r 2 + a r 3 + ⋯ {\displaystyle \sum _{n=1}^{\infty...

{\displaystyle n} th truncation error of the infinite series. An example of a convergent series is the geometric series 1 + 1 2 + 1 4 + 1 8 + ⋯ + 1 2 k + ⋯ . {\displaystyle...

In mathematics, the geometric mean is a mean or average which indicates a central tendency of a finite collection of positive real numbers by using the...

power series as being like "polynomials of infinite degree", although power series are not polynomials in the strict sense. The geometric series formula...

generalization of a geometric series of real or complex numbers to a geometric series of operators. The generalized initial term of the series is the identity...

"values", one can justify that the series converges to 1/2. Treating Grandi's series as a divergent geometric series and using the same algebraic methods...

_{n=1}^{\infty }\left(1-(2i)^{n-1}\right)z^{-n}.} This series can be derived using geometric series as before, or by performing polynomial long division...

the second part of a geometric series. Archimedes dissects the area into infinitely many triangles whose areas form a geometric progression. He then computes...

physical world and its model provided by Euclidean geometry; presently a geometric space, or simply a space is a mathematical structure on which some geometry...

In probability theory and statistics, the geometric distribution is either one of two discrete probability distributions: The probability distribution...

exponential and geometric sequences. It can also be used to illustrate sigma notation. When expressed as exponents, the geometric series is: 20 + 21 + 22...

Matrix polynomials can be used to sum a matrix geometrical series as one would an ordinary geometric series, S = I + A + A 2 + ⋯ + A n {\displaystyle S=I+A+A^{2}+\cdots...

proved (for any integer t {\displaystyle t} ) by using the formula for geometric series: (using y = 1 − x {\displaystyle y=1-x} ) t = 1 + 1 + ⋯ + 1 ≥ 1 + y...

In geometry, the geometric median of a discrete point set in a Euclidean space is the point minimizing the sum of distances to the sample points. This...

In mathematics, the inequality of arithmetic and geometric means, or more briefly the AM–GM inequality, states that the arithmetic mean of a list of non-negative...

integer values of α. The negative binomial series includes the case of the geometric series, the power series 1 1 − x = ∑ n = 0 ∞ x n {\displaystyle {\frac...

geometric may also refer to: Geometric distribution of probability theory and statistics Geometric series, a mathematical series with a constant ratio between...

geometric algebra (also known as a Clifford algebra) is an algebra that can represent and manipulate geometrical objects such as vectors. Geometric algebra...

as a geometric series with the common ratio 1. For some other divergent geometric series, including Grandi's series with ratio −1, and the series 1 + 2...

sum of the arithmetic and geometric series as early as the 4th century BCE. Ācārya Bhadrabāhu uses the sum of a geometric series in his Kalpasūtra in 433 BCE...

geometric series, with the initial value being a = C, the multiplicative factor being 1 + i, with n terms. Applying the formula for geometric series,...

infinite series ⁠1/2⁠ + ⁠1/4⁠ + ⁠1/8⁠ + ⁠1/16⁠ + ··· is an elementary example of a geometric series that converges absolutely. The sum of the series is 1...

different series, marked the first appearance of infinite series other than the geometric series in mathematics. However, this achievement fell into obscurity...

_{n=1}^{\infty }2^{n-n\alpha }=\sum _{n=1}^{\infty }2^{(1-\alpha )n}} (ii) is a geometric series with ratio 2 ( 1 − α ) {\displaystyle 2^{(1-\alpha )}} . (ii) is finitely...

I. Motomura developed the geometric series model based on benthic community data in a lake. Within the geometric series each species' level of abundance...

000 = 0, and so ...999 = −1. Another derivation uses a geometric series. The infinite series implied by "...999" does not converge in the real numbers...