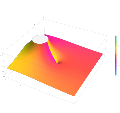
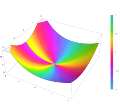
ordinary hypergeometric function 2F1(a,b;c;z) is a special function represented by the hypergeometric series, that includes many other special functions as...

a generalized hypergeometric series is a power series in which the ratio of successive coefficients indexed by n is a rational function of n. The series...

a confluent hypergeometric function is a solution of a confluent hypergeometric equation, which is a degenerate form of a hypergeometric differential...

mathematics, a general hypergeometric function or Aomoto–Gelfand hypergeometric function is a generalization of the hypergeometric function that was introduced...

random variable X {\displaystyle X} follows the hypergeometric distribution if its probability mass function (pmf) is given by p X ( k ) = Pr ( X = k ) =...

by elliptic hypergeometric series. A series xn is called hypergeometric if the ratio of successive terms xn+1/xn is a rational function of n. If the...

functions can be expressed in terms of the gamma function. More functions yet, including the hypergeometric function and special cases thereof, can be represented...

the beta function, also called the Euler integral of the first kind, is a special function that is closely related to the gamma function and to binomial...

Mittag-Leffler function, and can also be expressed as a confluent hypergeometric function (Kummer's function): erf ⁡ ( x ) = 2 x π M ( 1 2 , 3 2 , − x 2 ) . {\displaystyle...

}e^{-x\sinh t-\alpha t}\,dt.} The Bessel functions can be expressed in terms of the generalized hypergeometric series as J α ( x ) = ( x 2 ) α Γ ( α +...

generalization resembles the hypergeometric function and the Meijer G function but it belongs to a different class of functions. When r1 = r2, both sides...

of its kind: the generalized hypergeometric function and the MacRobert E-function had the same aim, but Meijer's G-function was able to include those as...

Sena Monteiro. "On the Relation between Lambert W-Function and Generalized Hypergeometric Functions". Researchgate. Retrieved 1 March 2023. (Srivastava...

{z^{s+k}}{s+k}}={\frac {z^{s}}{s}}M(s,s+1,-z),} where M is Kummer's confluent hypergeometric function. When the real part of z is positive, γ ( s , z ) = s − 1 z s e...

mathematics, the hypergeometric function of a matrix argument is a generalization of the classical hypergeometric series. It is a function defined by an...

elliptic hypergeometric series is a series Σcn such that the ratio cn/cn−1 is an elliptic function of n, analogous to generalized hypergeometric series...

hypergeometric functions of the first kind. The conventional Hermite polynomials may also be expressed in terms of confluent hypergeometric functions...

In mathematics, the exponential function is the unique real function which maps zero to one and has a derivative everywhere equal to its value. The exponential...

function (also known as Fox–Wright Psi function, not to be confused with Wright Omega function) is a generalisation of the generalised hypergeometric...

expressed in terms of the hypergeometric function, 2 F 1 {\displaystyle _{2}F_{1}} . With Γ {\displaystyle \Gamma } being the gamma function, the first solution...

bilateral hypergeometric series is a series Σan summed over all integers n, and such that the ratio an/an+1 of two terms is a rational function of n. The...

of which these functions are solutions, and found various reduction formulas and expressions of these series in terms of hypergeometric series of one variable...

mathematics, hypergeometric identities are equalities involving sums over hypergeometric terms, i.e. the coefficients occurring in hypergeometric series. These...

} Another connexion with the confluent hypergeometric functions is that E1 is an exponential times the function U(1,1,z): E 1 ( z ) = e − z U ( 1 , 1 ...

group is given by the hypergeometric series; furthermore, the spherical harmonics can be re-expressed in terms of the hypergeometric series, as SO(3) = PSU(2)...

hypergeometric function is an example of a four-argument function. The number of arguments that a function takes is called the arity of the function....

{1}{(1-t)^{\alpha +1}}}e^{-tx/(1-t)}.} Laguerre functions are defined by confluent hypergeometric functions and Kummer's transformation as L n ( α ) ( x...

function Riesz function Hypergeometric functions: Versatile family of power series. Confluent hypergeometric function Associated Legendre functions Meijer G-function...

potential and can be written in terms of confluent hypergeometric functions or Whittaker functions of imaginary argument. The Coulomb wave equation for...

mathematics, a Whittaker function is a special solution of Whittaker's equation, a modified form of the confluent hypergeometric equation introduced by...