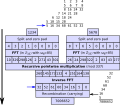
Modular exponentiation is exponentiation performed over a modulus. It is useful in computer science, especially in the field of public-key cryptography...

In mathematics, exponentiation, denoted bn, is an operation involving two numbers: the base, b, and the exponent or power, n. When n is a positive integer...

discrete logarithm problem. The computation of ga mod p is known as modular exponentiation and can be done efficiently even for large numbers. Note that g...

square-and-multiply algorithms or binary exponentiation. These can be of quite general use, for example in modular arithmetic or powering of matrices. For...

Algorithm (IDEA), and RC4. RSA and Diffie–Hellman use modular exponentiation. In computer algebra, modular arithmetic is commonly used to limit the size of...

U 2 j {\displaystyle U^{2^{j}}} . This can be accomplished via modular exponentiation, which is the slowest part of the algorithm. The gate thus defined...

well-studied at the time. Moreover, like Diffie-Hellman, RSA is based on modular exponentiation. Ron Rivest, Adi Shamir, and Leonard Adleman at the Massachusetts...

Regardless of the specific algorithm used, this operation is called modular exponentiation. For example, consider Z17×. To compute 3 4 {\displaystyle 3^{4}}...

primality test. Both the provable and probable primality tests rely on modular exponentiation. To further reduce the computational cost, the integers are first...

a} ⁠ randomly from 2 through p − 2 {\displaystyle p-2} and uses modular exponentiation to check whether a ( p − 1 ) / 2 ± 1 {\displaystyle a^{(p-1)/2}\pm...

provide equivalent security, compared to cryptosystems based on modular exponentiation in Galois fields, such as the RSA cryptosystem and ElGamal cryptosystem...

Standard for digital signatures, based on the mathematical concept of modular exponentiation and the discrete logarithm problem. In a digital signature system...

is known. The relative cost of exponentiation. Though it can be implemented more efficiently using modular exponentiation, when large values of m are involved...

However, when performing many multiplications in a row, as in modular exponentiation, intermediate results can be left in Montgomery form. Then the initial...

{n}}.} Here the matrix power Am is calculated using modular exponentiation, which can be adapted to matrices. A Fibonacci prime is a Fibonacci...

return composite return probably prime Using fast algorithms for modular exponentiation, the running time of this algorithm is O(k·log3 n), where k is the...

carry out these modular exponentiations, one could use a fast exponentiation algorithm like binary or addition-chain exponentiation). The algorithm can...

are coprime. With that provision, x is the modular multiplicative inverse of a modulo b, and y is the modular multiplicative inverse of b modulo a. Similarly...

respectively, hence testing them adds no value. Using fast algorithms for modular exponentiation and multiprecision multiplication, the running time of this algorithm...

theorem, characterizing even perfect numbers Euler's theorem, on modular exponentiation Euler's partition theorem relating the product and series representations...

mathematically speaking, multiplication of natural numbers is just "exponentiation in the additive monoid", this multiplication method can also be recognised...

46}).} Van Meter, Rodney; Itoh, Kohei M. (2005). "Fast Quantum Modular Exponentiation". Physical Review. 71 (5): 052320. arXiv:quant-ph/0408006. Bibcode:2005PhRvA...

Euclidean Lehmer's Modular square root Cipolla Pocklington's Tonelli–Shanks Berlekamp Other algorithms Chakravala Cornacchia Exponentiation by squaring Integer...

Euclidean Lehmer's Modular square root Cipolla Pocklington's Tonelli–Shanks Berlekamp Other algorithms Chakravala Cornacchia Exponentiation by squaring Integer...

Gauss' approach to modular arithmetic in 1801. Modulo (mathematics), general use of the term in mathematics Modular exponentiation Turn (angle) Mathematically...

is based on the assumption that this Rabin function is one-way. Modular exponentiation can be done in polynomial time. Inverting this function requires...

Euclidean Lehmer's Modular square root Cipolla Pocklington's Tonelli–Shanks Berlekamp Other algorithms Chakravala Cornacchia Exponentiation by squaring Integer...

computed as a term of certain Lucas sequence, instead of using modular exponentiation as in RSA or Diffie–Hellman. However, a paper by Bleichenbacher...

block and stream ciphers Modulo (mathematics) Modular arithmetic Modulo operation Modular exponentiation MOD., a science museum at the University of South...

little theorem. This is widely used in modular arithmetic, because this allows reducing modular exponentiation with large exponents to exponents smaller...