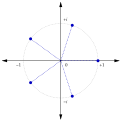
mathematics, a root of unity is any complex number that yields 1 when raised to some positive integer power n. Roots of unity are used in many branches of mathematics...

In mathematics, a principal n-th root of unity (where n is a positive integer) of a ring is an element α {\displaystyle \alpha } satisfying the equations...

In number theory, a kth root of unity modulo n for positive integers k, n ≥ 2, is a root of unity in the ring of integers modulo n; that is, a solution...

determining cases where a Gauss sum is the square root of a prime number, multiplied by a root of unity. It was proved and published independently by Sarvadaman...

changing the choice of the cube root in the definition of C, or, equivalently by multiplying C by a primitive cube root of unity, that is ⁠–1 ± √–3/2⁠...

principal nth root of unity, defined by: The discrete Fourier transform maps an n-tuple ( v 0 , … , v n − 1 ) {\displaystyle (v_{0},\ldots ,v_{n-1})} of elements...

Heckenberger: Nichols algebras of diagonal type and arithmetic root systems, Habilitation thesis 2005. Heckenberger, Schneider: Root system and Weyl gruppoid...

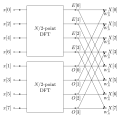
D {\displaystyle D} th root of unity modulo 2 n ′ + 1 {\displaystyle 2^{n'}+1} . We now take the discrete Fourier transform of the arrays A , B {\displaystyle...

the field of the rational numbers of any primitive nth-root of unity ( e 2 i π / n {\displaystyle e^{2i\pi /n}} is an example of such a root). An important...

mathematics, a primitive root may mean: Primitive root modulo n in modular arithmetic Primitive nth root of unity amongst the solutions of zn = 1 in a field...

root of unity with the smallest positive argument, it is called the principal primitive nth root of unity, sometimes shortened as principal nth root of...

exactly the elements of Cp of the form pr·ζ where r is a rational number and ζ is a root of unity. Note that there is no analogue in Cp of Euler's identity...

primitive root modulo n (or in fuller language primitive root of unity modulo n, emphasizing its role as a fundamental solution of the roots of unity polynomial...

α and all of its conjugates in the complex numbers have absolute value at most 1, then α is a root of unity. There are quantitative forms of this, stating...

a field of characteristic p {\displaystyle p} , every n p {\displaystyle np} th root of unity is also a n {\displaystyle n} th root of unity. It follows...

primitive element if it is a primitive (q − 1)th root of unity in GF(q); this means that each non-zero element of GF(q) can be written as αi for some natural...

complex root of unity to Q {\displaystyle \mathbb {Q} } , the field of rational numbers. Cyclotomic fields played a crucial role in the development of modern...

algebraic number field with ring of integers O k {\displaystyle {\mathcal {O}}_{k}} that contains a primitive n-th root of unity ζ n . {\displaystyle \zeta...

above. Apotome (mathematics) Cube root Functional square root Integer square root Nested radical Nth root Root of unity Solving quadratic equations with...

mathematician and engineer Heron of Alexandria is noted as the first to present a calculation involving the square root of a negative number, it was Rafael...

always abelian. If a field K contains a primitive n-th root of unity and the n-th root of an element of K is adjoined, the resulting Kummer extension is an...

{-1+i{\sqrt {3}}}{2}}=e^{i2\pi /3}} is a primitive (hence non-real) cube root of unity. The Eisenstein integers form a triangular lattice in the complex plane...

that e − 2 π i / n {\textstyle e^{-2\pi i/n}} is an n'th primitive root of unity, and thus can be applied to analogous transforms over any finite field...

cyclic (see Root of unity § Cyclic groups). In addition to the multiplication of two elements of F, it is possible to define the product n ⋅ a of an arbitrary...

the entire field GF(pm). This implies that α is a primitive (pm − 1)-root of unity in GF(pm). Because all minimal polynomials are irreducible, all primitive...

Methods of computing square roots List of polynomial topics Nth root Square root Nested radical Root of unity "In Search of a Fast Cube Root". metamerist...

of degree n is the extension of it by a primitive nth root of unity, and that the Galois group of the nth roots of unity is cyclic. Lang, Serge (2002)...

2 10 , {\displaystyle x=\pm r{\sqrt[{10}]{2}},} where r is a fifth root of unity, which can be expressed with two nested square roots. See also Quintic...

2\cos(2\pi /n).} The roots of the minimal polynomial are twice the real part of the roots of unity, where the real part of a root of unity is just cos ⁡ ( 2 k...

circular unit) is a unit of an algebraic number field which is the product of numbers of the form (ζa n − 1) for ζ n an nth root of unity and 0 < a < n. The...