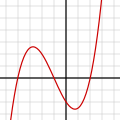
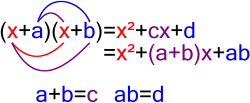In mathematics, the Abel–Ruffini theorem (also known as Abel's impossibility theorem) states that there is no solution in radicals to general polynomial...

(Abel–Ruffini theorem) that quintic (and higher-order) equations cannot be solved by radicals (1799). Abel would complete the proof in 1824. Ruffini's...

the four basic arithmetic operations. This widely generalizes the Abel–Ruffini theorem, which asserts that a general polynomial of degree at least five...

By 1823, Abel had at last proved the impossibility of solving the quintic equation in radicals (now referred to as the Abel–Ruffini theorem). However...

symmetries of field extensions, provides an elegant proof of the Abel–Ruffini theorem that general quintic equations cannot be solved in radicals. Fields...

(fourth-degree) equations, but not for higher-degree equations, by the Abel–Ruffini theorem.) trigonometrically numerical approximations of the roots can be...

equations are generally impossible to solve in terms of radicals (see Abel–Ruffini theorem). This particular equation, however, may be written ( x 3 ) 2 − 9...

equation in M2 and, though some of these may be solved explicitly, the Abel–Ruffini theorem guarantees that there exists no general form for the roots of these...

saying that the polynomial x2 + ax + b has no real roots). (By the Abel–Ruffini theorem, the real numbers a and b are not necessarily expressible in terms...

the impossibility of such a general solution was proved with the Abel–Ruffini theorem. Finding the roots (zeros) of a given polynomial has been a prominent...

formulas for the cubic and quartic equations. For higher degrees, the Abel–Ruffini theorem asserts that there can not exist a general formula in radicals. However...

generally cannot be computed in terms of radicals (nth roots), by the Abel–Ruffini theorem. In most cases, the best that can be done is computing approximate...

Septic function Octic function Completing the square Abel–Ruffini theorem Bring radical Binomial theorem Blossom (functional) Root of a function nth root...

however, cannot be expressed by such finite expressions (this is the Abel–Ruffini theorem). This is the case, for example, for the Bring radical, which is...

theorem (number theory) Wolstenholme's theorem (number theory) Zeckendorf's theorem (number theory) Zsigmondy's theorem (number theory) Abel–Ruffini theorem...

solutions for higher degrees, as proven in the 19th century by the Abel–Ruffini theorem. Even when general solutions do not exist, approximate solutions...

which contain a fourth degree (but no higher) polynomial are, by the Abel–Ruffini theorem, the highest degree equations having a general solution using radicals...

polynomial equation can be solved by radicals, according to the Abel–Ruffini theorem. Lodovico Ferrari is credited with the discovery of the solution...

if the degree n {\displaystyle n} is 4 or less. According to the Abel–Ruffini theorem there is no general, explicit and exact algebraic formula for the...

equations, which are more complicated than the quadratic formula. The Abel–Ruffini theorem,: 211  and, more generally Galois theory, state that some quintic...

Abel–Ruffini theorem was nearly proved by Paolo Ruffini, but his proof, spanning 500 pages, was mostly ignored and later, in 1824, Niels Henrik Abel published...

with the degree, limiting their usefulness. In higher degrees, the Abel–Ruffini theorem states that there are equations whose solutions cannot be expressed...

higher degree equations was an important development, the Abel–Ruffini theorem (Ruffini 1799, Abel 1824) showed that they could not be solved by radicals...

splitting field of f over K contained in a radical extension of K. The Abel–Ruffini theorem states that such a solution by radicals does not exist, in general...

but to a non elementary transformation. This was proven by the Abel–Ruffini theorem and by the Galois theory too. Every power of a nome of a positive...

n 5 ( mod 10 ) {\displaystyle n\equiv n^{5}{\pmod {10}}} By the Abel–Ruffini theorem, there is no general algebraic formula (formula expressed in terms...

method for solving polynomial equations of degree greater than four (Abel–Ruffini theorem). Other 19th-century mathematicians used this in their proofs that...

not. This is the Abel–Ruffini theorem. The ring of algebraic integers is a Bézout domain, as a consequence of the principal ideal theorem. If the monic polynomial...

their order are greater than p ( p − 1 ) . {\displaystyle p(p-1).} Abel–Ruffini theorem results from this and the fact that there are polynomials with a...

solvable by radicals (Abel–Ruffini theorem). This property is also used in complexity theory in the proof of Barrington's theorem. Consider the subgroups...