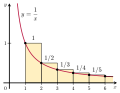
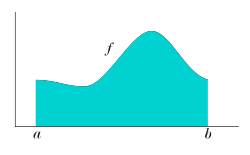
In mathematics, the Cauchy condensation test, named after Augustin-Louis Cauchy, is a standard convergence test for infinite series. For a non-increasing...

specialized convergence tests, for instance for Fourier series there is the Dini test. Consider the series Cauchy condensation test implies that (i) is finitely...

in the 14th century by Nicole Oresme using a precursor to the Cauchy condensation test for the convergence of infinite series. It can also be proven to...

that is still taught. Also Cauchy's well-known test for absolute convergence stems from this book: Cauchy condensation test. In 1829 he defined for the...

Cauchy's test may refer to: Cauchy's root test Cauchy's condensation test the integral test for convergence, sometimes known as the Maclaurin–Cauchy test...

developed by Colin Maclaurin and Augustin-Louis Cauchy and is sometimes known as the Maclaurin–Cauchy test. Consider an integer N and a function f defined...

divergence of the harmonic series, and it is the basis for the general Cauchy condensation test. In ordinary finite summations, terms of the summation can be rearranged...

completeness Cauchy condensation test Cauchy's convergence test Cauchy–Hadamard theorem Cauchy product Cauchy's radical test Cauchy ratio test Cauchy sequence Uniformly...

as the Cauchy root test or Cauchy's radical test. For a series ∑ n = 1 ∞ a n {\displaystyle \sum _{n=1}^{\infty }a_{n}} the root test uses the number C...

and has a limit of 0 at infinity, then the series converges. Cauchy condensation test. If { a n } {\displaystyle \left\{a_{n}\right\}} is a positive...

simplest version of the term test applies to infinite series of real numbers. The above two proofs, by invoking the Cauchy criterion or the linearity of...

large. The test was first published by Jean le Rond d'Alembert and is sometimes known as d'Alembert's ratio test or as the Cauchy ratio test. The usual...

value theorem in its modern form was stated and proved by Augustin Louis Cauchy in 1823. Many variations of this theorem have been proved since then. Let...

mathematics, Abel's test (also known as Abel's criterion) is a method of testing for the convergence of an infinite series. The test is named after mathematician...

is a Cauchy sequence, and so must converge to a limit. Therefore, ∑ a n {\displaystyle \sum a_{n}} is absolutely convergent. The comparison test for integrals...

In mathematics, Dirichlet's test is a method of testing for the convergence of a series that is especially useful for proving conditional convergence...

test proves that an alternating series is convergent when its terms decrease monotonically in absolute value and approach zero in the limit. The test...

Convergence tests Summand limit (term test) Ratio Root Integral Direct comparison Limit comparison Alternating series Cauchy condensation Dirichlet Abel...

Convergence tests Summand limit (term test) Ratio Root Integral Direct comparison Limit comparison Alternating series Cauchy condensation Dirichlet Abel...

Convergence tests Summand limit (term test) Ratio Root Integral Direct comparison Limit comparison Alternating series Cauchy condensation Dirichlet Abel...

Convergence tests Summand limit (term test) Ratio Root Integral Direct comparison Limit comparison Alternating series Cauchy condensation Dirichlet Abel...

Convergence tests Summand limit (term test) Ratio Root Integral Direct comparison Limit comparison Alternating series Cauchy condensation Dirichlet Abel...

Convergence tests Summand limit (term test) Ratio Root Integral Direct comparison Limit comparison Alternating series Cauchy condensation Dirichlet Abel...

complex-valued function along a curve in the complex plane application of the Cauchy integral formula application of the residue theorem One method can be used...

Convergence tests Summand limit (term test) Ratio Root Integral Direct comparison Limit comparison Alternating series Cauchy condensation Dirichlet Abel...

Convergence tests Summand limit (term test) Ratio Root Integral Direct comparison Limit comparison Alternating series Cauchy condensation Dirichlet Abel...

and taking the limit yields a term which is bounded from above by the Cauchy-Schwarz inequality | ∇ v f ( x ) | = | ∇ f ⋅ v | ≤ | ∇ f | | v | = | ∇ f...

variables are holomorphic functions, that is, solutions to the n-dimensional Cauchy–Riemann conditions, we usually look on the part of the Hessian that contains...

Frédéric Sarrus (1842) which was condensed and improved by Augustin-Louis Cauchy (1844). Other valuable treatises and memoirs have been written by Strauch[which...

Convergence tests Summand limit (term test) Ratio Root Integral Direct comparison Limit comparison Alternating series Cauchy condensation Dirichlet Abel...