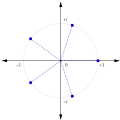
mathematics, the complex conjugate root theorem states that if P is a polynomial in one variable with real coefficients, and a + bi is a root of P with a and...

a root of a univariate polynomial with real coefficients is complex, then its complex conjugate is also a root. The complex conjugate of a complex number...

coefficients (this is the complex conjugate root theorem). Conversely, if one has a factor of degree two, the quadratic formula gives a root. Every univariate...

[L:K(α)]sep. A theorem of Kronecker states that if α is a nonzero algebraic integer such that α and all of its conjugates in the complex numbers have absolute...

electrical circuits, the complex conjugate is used in finding the equivalent impedance when the maximum power transfer theorem is looked for. Three non-collinear...

square roots Cube root Root of unity Constructible number Complex conjugate root theorem Algebraic element Horner scheme Rational root theorem Gauss's lemma...

exponents. In particular, the reciprocal of an nth root of unity is its complex conjugate, and is also an nth root of unity: 1 z = z − 1 = z n − 1 = z ¯ . {\displaystyle...

scalars is the complex numbers. By the fundamental theorem of algebra, applied to the characteristic polynomial of A, there is at least one complex eigenvalue...

Rouché's theorem, named after Eugène Rouché, states that for any two complex-valued functions f and g holomorphic inside some region K {\displaystyle...

In complex analysis, the Riemann mapping theorem states that if U {\displaystyle U} is a non-empty simply connected open subset of the complex number...

simple root of the characteristic polynomial. (These requirements hold for primitive matrices as above). Given that M is diagonalizable, M is conjugate to...

vanishes. If E is a complex vector bundle, then the conjugate bundle E ¯ {\displaystyle {\overline {E}}} of E is obtained by having complex numbers acting...

domain. That all holomorphic functions are complex analytic functions, and vice versa, is a major theorem in complex analysis. Holomorphic functions are also...

including points at infinity and points with complex coordinates. In its modern formulation, the theorem states that, if N is the number of common points...

element) of order p in G. Theorem (2)—Given a finite group G and a prime number p, all Sylow p-subgroups of G are conjugate to each other. That is, if...

In complex analysis, Liouville's theorem, named after Joseph Liouville (although the theorem was first proven by Cauchy in 1844), states that every bounded...

Abel-Ruffini theorem. On the other hand, the fundamental theorem of algebra shows that all nonconstant polynomials have at least one root. Therefore, root-finding...

In complex analysis, a branch of mathematics, the Gauss–Lucas theorem gives a geometric relation between the roots of a polynomial P and the roots of its...

the coefficients can be ill-conditioned for many inputs. The complex conjugate root theorem states that if the coefficients of a polynomial are real, then...

{\displaystyle {\overline {\gamma '(z)}}} , and the complex inner product would attribute twice a conjugate to γ ′ {\displaystyle \gamma '} in the vector field...

symmetric polynomial whose arguments are all conjugates of one another gives a rational number. The theorem is named for Ferdinand von Lindemann and Karl...

In complex analysis, a branch of mathematics, Morera's theorem, named after Giacinto Morera, gives a criterion for proving that a function is holomorphic...

\mathbf {x} .} More generally, a Hermitian matrix (that is, a complex matrix equal to its conjugate transpose) is positive-definite if the real number z ∗ M...

In mathematics, a zero (also sometimes called a root) of a real-, complex-, or generally vector-valued function f {\displaystyle f} , is a member x {\displaystyle...

coefficients, it follows that its roots appear in complex conjugate pairs, that is, if α is a root then so is α∗. There are 3 roots, thus at least one...

{\displaystyle A=B^{\textsf {T}}B} are equivalent. For complex-valued matrices, the conjugate transpose B ∗ {\displaystyle B^{*}} is used instead and...

method Euler method Fast inverse square root Fisher scoring Gradient descent Integer square root Kantorovich theorem Laguerre's method Methods of computing...

In mathematics, Wedderburn's little theorem states that every finite division ring is a field; thus, every finite domain is a field. In other words, for...

arguments, and the value of the function at the complex conjugate of z {\displaystyle z} will be the complex conjugate of the value at z   . {\displaystyle z~...

norm of a quaternion (the square root of the product with its conjugate, as with complex numbers) is the square root of the determinant of the corresponding...