In number theory, two integers a and b are coprime, relatively prime or mutually prime if the only positive integer that is a divisor of both of them...
16 KB (2,386 words) - 15:43, 27 April 2025
the integers coprime (relatively prime) to n from the set { 0 , 1 , … , n − 1 } {\displaystyle \{0,1,\dots ,n-1\}} of n non-negative integers form a...
26 KB (3,156 words) - 13:35, 6 May 2025
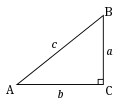
An integer triangle or integral triangle is a triangle all of whose side lengths are integers. A rational triangle is one whose side lengths are rational...
41 KB (7,271 words) - 18:57, 19 June 2025
P-adic number (redirect from P-adic integers)
{\displaystyle k} is a (possibly negative) integer, n {\displaystyle n} and d {\displaystyle d} are coprime integers both coprime with p {\displaystyle p} , and d...
44 KB (7,716 words) - 17:25, 28 May 2025
Rational number (section Embedding of integers)
fraction a b , {\displaystyle {\tfrac {a}{b}},} where a and b are coprime integers and b > 0. This is often called the canonical form of the rational...
24 KB (3,391 words) - 07:07, 16 June 2025
n_{k}} be k pairwise coprime integers greater than one, a 1 , … , a k {\displaystyle a_{1},\dots ,a_{k}} be k arbitrary integers, and N be the product...
33 KB (4,809 words) - 12:42, 14 May 2025
Parametric equation (section Integer geometry)
parameters m and n are positive coprime integers that are not both odd. By multiplying a, b and c by an arbitrary positive integer, one gets a parametrization...
20 KB (2,909 words) - 14:11, 22 April 2025
c=k\cdot (m^{2}+n^{2})} where m, n, and k are positive integers with m > n, and with m and n coprime and not both odd. That these formulas generate Pythagorean...
82 KB (11,398 words) - 23:28, 20 June 2025
Euclidean algorithm (section Gaussian integers)
as an ideal in the ring of integers, which is closely related to GCD. If gcd(a, b) = 1, then a and b are said to be coprime (or relatively prime). This...
126 KB (15,349 words) - 16:35, 30 April 2025
whose leading coefficient is 1) whose coefficients are integers. The set of all algebraic integers A is closed under addition, subtraction and multiplication...
12 KB (1,499 words) - 19:23, 5 June 2025
Modular arithmetic (redirect from Integers mod n)
multiplicative group of the integers modulo m that are invertible. It consists of the congruence classes am, where a is coprime to m; these are precisely...
29 KB (3,646 words) - 13:08, 26 June 2025
Each torus knot is specified by a pair of coprime integers p and q. A torus link arises if p and q are not coprime (in which case the number of components...
16 KB (1,783 words) - 12:35, 30 June 2025
which the sum of two coprime integers, each a power of an integer, with the powers not necessarily equal, can equal another integer that is a power, with...
5 KB (832 words) - 22:47, 19 June 2025
of values (am, bn, ck), where a, b, c are positive coprime integers and m, n, k are positive integers satisfying The statement is about the finiteness of...
103 KB (11,708 words) - 08:55, 30 June 2025
\text{rad}}(2^{6}\cdot 5^{6})=2\cdot 5=10} If a, b, and c are coprime positive integers such that a + b = c, it turns out that "usually" c < rad ( a b...
42 KB (4,598 words) - 08:53, 30 June 2025
any two positive coprime integers a and d, there are infinitely many primes of the form a + nd, where n is also a positive integer. In other words, there...
24 KB (3,526 words) - 22:13, 17 June 2025
degree two with integer coefficients. Because of the homogeneity, one can consider only parameters that are setwise coprime integers. If Q ( X 0 , … ...
41 KB (7,423 words) - 17:19, 10 April 2025
Extended Euclidean algorithm (section Modular integers)
the greatest common divisor (gcd) of integers a and b, also the coefficients of Bézout's identity, which are integers x and y such that a x + b y = gcd (...
28 KB (4,467 words) - 20:39, 9 June 2025
of values (am, bn, ck) where a, b, c are positive coprime integers and m, n, k are positive integers satisfying The inequality on m, n, and k is a necessary...
5 KB (710 words) - 10:08, 25 May 2025
Formulas for generating Pythagorean triples (section Generating all Pythagorean triples using a predetermined positive integer)
Start with a 2 × 2 array and insert two coprime positive integers (q,q′) in the top row. Place the even integer (if any) in the left-hand column. [ q q...
30 KB (4,539 words) - 09:33, 5 June 2025
Shor's algorithm (category Integer factorization algorithms)
algorithm is known that can factor integers in polynomial time. However, Shor's algorithm shows that factoring integers is efficient on an ideal quantum...
40 KB (5,812 words) - 21:44, 17 June 2025
states that if x and y are coprime integers (i.e. they share no common divisors other than 1 and −1) there exist integers r and s such that r x + s y...
15 KB (1,796 words) - 21:28, 8 April 2025
division of an integer n by several integers, then one can determine uniquely the remainder of the division of n by the product of these integers, under the...
43 KB (7,239 words) - 03:37, 18 May 2025
{\displaystyle a+nd,\ } where n runs through the positive integers and a and d are any given positive coprime integers with 1 ≤ a ≤ d − 1, then: p ( a , d ) < c d...
9 KB (851 words) - 16:15, 8 February 2025
theorem or Euler's totient theorem) states that, if n and a are coprime positive integers, then a φ ( n ) {\displaystyle a^{\varphi (n)}} is congruent to...
9 KB (1,149 words) - 18:09, 9 June 2024
decomposition of a positive integer into a product of integers. Every positive integer greater than 1 is either the product of two or more integer factors greater...
25 KB (2,977 words) - 21:02, 19 June 2025
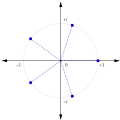
Root of unity (section Relation to quadratic integers)
the primitive nth roots of unity are those for which k and n are coprime integers. Subsequent sections of this article will comply with complex roots...
41 KB (5,944 words) - 19:06, 23 June 2025
(φ) function) in number theory, counting the number of coprime integers less than an integer. Euler hypergeometric integral Euler–Riemann zeta function...
15 KB (1,744 words) - 11:30, 13 June 2025
number theory, a Gaussian integer is a complex number whose real and imaginary parts are both integers. The Gaussian integers, with ordinary addition and...
35 KB (4,835 words) - 07:01, 5 May 2025
system (RNS) is a numeral system representing integers by their values modulo several pairwise coprime integers called the moduli. This representation is...
14 KB (1,597 words) - 11:30, 25 May 2025