precision, an integer relation algorithm will either find an integer relation between them, or will determine that no integer relation exists with coefficients...

the Euclidean algorithm, or Euclid's algorithm, is an efficient method for computing the greatest common divisor (GCD) of two integers, the largest number...

general algorithm for integer factorization, any integer can be factored into its constituent prime factors by repeated application of this algorithm. The...

Euclidean algorithm is an extension to the Euclidean algorithm, and computes, in addition to the greatest common divisor (gcd) of integers a and b, also...

The algorithm can be used to find integer solutions to many problems. In particular, the LLL algorithm forms a core of one of the integer relation algorithms...

Pollard's rho algorithm is an algorithm for integer factorization. It was invented by John Pollard in 1975. It uses only a small amount of space, and...

The Schönhage–Strassen algorithm is an asymptotically fast multiplication algorithm for large integers, published by Arnold Schönhage and Volker Strassen...

(reciprocal) licenses: MINTO (Mixed Integer Optimizer, an integer programming solver which uses branch and bound algorithm) has publicly available source code...

Shor's algorithm is a quantum algorithm for finding the prime factors of an integer. It was developed in 1994 by the American mathematician Peter Shor...

Let y {\displaystyle y} and k {\displaystyle k} be non-negative integers. Algorithms that compute (the decimal representation of) y {\displaystyle {\sqrt...

(GCD) of two nonnegative integers. Stein's algorithm uses simpler arithmetic operations than the conventional Euclidean algorithm; it replaces division with...

A division algorithm is an algorithm which, given two integers N and D (respectively the numerator and the denominator), computes their quotient and/or...

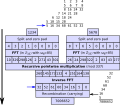
The Karatsuba algorithm is a fast multiplication algorithm for integers. It was discovered by Anatoly Karatsuba in 1960 and published in 1962. It is a...

optimal bound, although this remains a conjecture today. Integer multiplication algorithms can also be used to multiply polynomials by means of the method...

Pollard's p − 1 algorithm is a number theoretic integer factorization algorithm, invented by John Pollard in 1974. It is a special-purpose algorithm, meaning...

"ABC ABCDAB ABCDABCDABDE". At any given time, the algorithm is in a state determined by two integers: m, denoting the position within S where the prospective...

empty_list for k = 1 , 2 , … {\displaystyle k=1,2,\ldots } Using an integer factorization algorithm optimized for smooth numbers, try to factor g k mod q {\displaystyle...

discrete logarithms in a finite abelian group whose order is a smooth integer. The algorithm was introduced by Roland Silver, but first published by Stephen...

Institute Relation Locator) is a hypothetical hardware device designed to speed up the sieving step of the general number field sieve integer factorization...

theory, Williams's p + 1 algorithm is an integer factorization algorithm, one of the family of algebraic-group factorisation algorithms. It was invented by...

conquer), its running time is described by a recurrence relation. A simple example is the time an algorithm takes to find an element in an ordered vector with...

following algorithm (for a zero-based array). -- To shuffle an array a of n elements (indices 0..n-1): for i from n−1 down to 1 do j ← random integer such...

of distinct integers AND the integers are all in S AND the integers sum to 0 THEN OUTPUT "yes" and HALT This is a polynomial-time algorithm accepting an...

Gaussian integers share many properties with integers: they form a Euclidean domain, and thus have a Euclidean division and a Euclidean algorithm; this implies...

binary relation Traveling salesman problem Christofides algorithm Nearest neighbour algorithm Vehicle routing problem Clarke and Wright Saving algorithm Warnsdorff's...

an integer n ≥ 1 such that fn(k) = 1. In 1972, John Horton Conway proved that a natural generalization of the Collatz problem is algorithmically undecidable...

calculated through the Euclidean algorithm, since lcm(a, b) = ⁠|ab|/gcd(a, b)⁠. λ(n) is kept secret. Choose an integer e such that 1 < e < λ(n) and gcd(e...

to many digits, and then using an integer relation-finding algorithm (typically Helaman Ferguson's PSLQ algorithm) to find a sequence A that adds up...

integer (possibly negative), and each a i {\displaystyle a_{i}} is an integer such that 0 ≤ a i < p . {\displaystyle 0\leq a_{i}<p.} A p-adic integer...

if there is an integer k such that a − b = k m. Congruence modulo m is a congruence relation, meaning that it is an equivalence relation that is compatible...