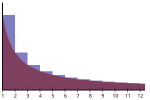
In mathematics, the Stieltjes constants are the numbers γ k {\displaystyle \gamma _{k}} that occur in the Laurent series expansion of the Riemann zeta...

Riemann–Stieltjes integral Stieltjes constants Stieltjes matrix Stieltjes moment problem Stieltjes polynomials Stieltjes transformation (and Stieltjes inversion...

Weisstein, Eric W. "Stieltjes Constants". mathworld.wolfram.com. Retrieved 2024-11-01. Finch, Steven R. (2003-08-18). Mathematical Constants. Cambridge University...

"Copeland–Erdős Constant Continued Fraction". MathWorld. "Hermite Constants". Weisstein, Eric W. "Relatively Prime". MathWorld. "Favard Constants". OEIS: A000796...

\gamma } is the Euler–Mascheroni constant. These t n {\displaystyle t_{n}} play the analog of the Stieltjes constants, but for the falling factorial expansion...

_{n=0}^{\infty }{\frac {\gamma _{n}}{n!}}(1-s)^{n}.} The constants γn here are called the Stieltjes constants and can be defined by the limit γ n = lim m → ∞ (...

The Laurent series expansion can be used to define generalized Stieltjes constants that occur in the series ζ ( s , a ) = 1 s − 1 + ∑ n = 0 ∞ ( − 1...

gamma function, the polygamma functions, the Stieltjes constants and many other special functions and constants may be expressed in terms of infinite series...

MR 0036882. Johansson, F.; Blagouchine, Ia. (2019), "Computing Stieltjes constants using complex integration", Mathematics of Computation, 88 (318):...

formula. This theorem has also been called the Stieltjes–Osgood theorem, after Thomas Joannes Stieltjes and William Fogg Osgood. The Corollary stated above...

In mathematics, Stieltjes–Wigert polynomials (named after Thomas Jan Stieltjes and Carl Severin Wigert) are a family of basic hypergeometric orthogonal...

Malmsten's integrals are also found to be closely connected to the Stieltjes constants. In 1842, Malmsten also evaluated several important logarithmic series...

\atop m+1}\right]\left[{n \atop 2k+1}\right]\,} where γm are the Stieltjes constants and δm,0 represents the Kronecker delta function. Notice that this...

odd zeta constants ζ(2n + 1) are irrational. In particular at least one of ζ(5), ζ(7), ζ(9), and ζ(11) must be irrational. Apéry's constant has not yet...

B_{1}\approx 0.26149721} is the Mertens constant and γ j {\displaystyle \gamma _{j}} are the Stieltjes constants. The function ω ( n ) {\displaystyle \omega...

"A theorem for the closed-form evaluation of the first generalized Stieltjes constant at rational arguments and some related summations". Journal of Number...

products. The Lebesgue–Stieltjes integral is the ordinary Lebesgue integral with respect to a measure known as the Lebesgue–Stieltjes measure, which may be...

"A theorem for the closed-form evaluation of the first generalized Stieltjes constant at rational arguments and some related summations". Journal of Number...

the Riemann–Stieltjes integral, and where F {\displaystyle F} is the cumulative distribution function. This is simply the Laplace-Stieltjes transform of...

. Kalugin, German A.; Jeffrey, David J.; Corless, Robert M. (2011). "Stieltjes, Poisson and other integral representations for functions of Lambert W"...

Riemann integral can be regarded as the special case where we only allow constant gauges. Let f : [ a , b ] ↦ R {\displaystyle f:[a,b]\mapsto \mathbb {R}...

the Itô stochastic integral, a stochastic generalization of the Riemann–Stieltjes integral in analysis. The integrands and the integrators are now stochastic...

and related branches of mathematics, the Lebesgue–Stieltjes integral generalizes Riemann–Stieltjes and Lebesgue integration, preserving the many advantages...

between the zeta functions, as well as in various formulas for the Stieltjes constants, e.g. γ m ( v ) = − ln m + 1 ⁡ ( v + a ) m + 1 + ∑ n = 0 ∞ ( − 1...

{\pi }{2}}.} The (unilateral) Laplace–Stieltjes transform of a function g : ℝ → ℝ is defined by the Lebesgue–Stieltjes integral { L ∗ g } ( s ) = ∫ 0 ∞ e...

Fourier–Stieltjes transform of its distribution measure, but in this context it is typical to take a different convention for the constants. Typically...

Chebyshev rational functions Chebyshev–Gauss quadrature Chebyshev–Markov–Stieltjes inequalities Chebyshev's bias Chebyshev's inequality in probability and...

Hermite; letter to Thomas Joannes Stieltjes about Weierstrass functions, Correspondance d'Hermite et de Stieltjes vol.2, p.317-319 In addition to the...

> 1 {\displaystyle {\frac {1}{p}}+{\frac {1}{q}}>1} then the Riemann–Stieltjes Integral ∫ a b f ( x ) d g ( x ) := lim | D | → 0 ∑ t k ∈ D f ( t k )...

functions Moment-generating functions Laplace transforms and Laplace–Stieltjes transforms Characteristic functions A proof of the central limit theorem...