with conservation of energy and momentum. The Einstein tensor G {\displaystyle {\boldsymbol {G}}} is a tensor of order 2 defined over pseudo-Riemannian manifolds...

tensor of spacetime for a given arrangement of stress–energy–momentum in the spacetime. The relationship between the metric tensor and the Einstein tensor...

Riemann curvature tensor, the Weyl tensor expresses the tidal force that a body feels when moving along a geodesic. The Weyl tensor differs from the Riemann...

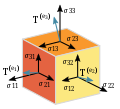
stress-energy tensor The stress–energy tensor, sometimes called the stress–energy–momentum tensor or the energy–momentum tensor, is a tensor physical quantity...

The Einstein tensor is built up from the metric tensor and its partial derivatives; thus, given the stress–energy tensor, the Einstein field equations...

the Einstein convention is that it applies to other vector spaces built from V using the tensor product and duality. For example, V ⊗ V, the tensor product...

(electromagnetic tensor, Maxwell tensor, permittivity, magnetic susceptibility, ...), and general relativity (stress–energy tensor, curvature tensor, ...). In...

formulation of spin (the spin tensor). These extra equations express the torsion linearly in terms of the spin tensor associated with the matter source...

manifold M {\displaystyle M} and the metric tensor is given as a covariant, second-degree, symmetric tensor on M {\displaystyle M} , conventionally denoted...

of tensor theory. For expositions of tensor theory from different points of view, see: Tensor Tensor (intrinsic definition) Application of tensor theory...

relationship between the Ricci tensor and the matter content of the universe. Like the metric tensor, the Ricci tensor assigns to each tangent space of...

mathematical field of differential geometry, the Riemann curvature tensor or Riemann–Christoffel tensor (after Bernhard Riemann and Elwin Bruno Christoffel) is the...

In mathematics and physics, a tensor field is a function assigning a tensor to each point of a region of a mathematical space (typically a Euclidean space...

Jordan–Brans–Dicke theory) is a competitor to Einstein's general theory of relativity. It is an example of a scalar–tensor theory, a gravitational theory in which...

the Ricci tensor. The Riemann curvature tensor can be expressed in terms of the covariant derivative. The Einstein tensor G is a rank-2 tensor defined over...

fact that the Einstein tensor vanishes if and only if the Ricci tensor vanishes. This follows from the fact that these two second rank tensors stand in a...

Einstein tensor, computed uniquely from the metric tensor which is part of the definition of a Lorentzian manifold. Since giving the Einstein tensor does...

differential geometry, a tensor density or relative tensor is a generalization of the tensor field concept. A tensor density transforms as a tensor field when passing...

notation and manipulation for tensors and tensor fields on a differentiable manifold, with or without a metric tensor or connection. It is also the modern...

G_{ab}} is the Einstein tensor, Λ {\displaystyle \Lambda } is the cosmological constant, g a b {\displaystyle g_{ab}} is the metric tensor, c {\displaystyle...

Pseudovector Spinor Tensor Tensor algebra, Free algebra Tensor contraction Symmetric algebra, Symmetric power Symmetric tensor Mixed tensor Pandey, Divyanshu;...

differential geometry, the torsion tensor is a tensor that is associated to any affine connection. The torsion tensor is a bilinear map of two input vectors...

Cotton tensor on a (pseudo)-Riemannian manifold of dimension n is a third-order tensor concomitant of the metric. The vanishing of the Cotton tensor for...

general relativity by Noether's prescriptions do not make a real tensor for this reason. Einstein argued that this is true for a fundamental reason: the gravitational...

An Einstein–Weyl geometry is a smooth conformal manifold, together with a compatible Weyl connection that satisfies an appropriate version of the Einstein...

metric field on M consists of a metric tensor at each point p of M that varies smoothly with p. A metric tensor g is positive-definite if g(v, v) > 0 for...

quanta are fermionic particles such as electrons, and tensor fields such as the metric tensor field that describes the shape of spacetime and gives rise...

solution is an exact solution to the Einstein field equation in which the only term in the stress–energy tensor is a cosmological constant term. This...

mathematics, the modern component-free approach to the theory of a tensor views a tensor as an abstract object, expressing some definite type of multilinear...

the metric tensor matrix, R {\displaystyle R} is the Ricci scalar, and κ = 8 π G c − 4 {\displaystyle \kappa =8\pi Gc^{-4}} is the Einstein gravitational...