In mathematics, a Coxeter group, named after H. S. M. Coxeter, is an abstract group that admits a formal description in terms of reflections (or kaleidoscopic...
35 KB (3,758 words) - 10:19, 16 October 2024
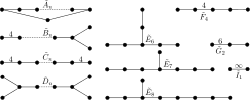
Coxeter–Dynkin diagram (or Coxeter diagram, Coxeter graph) is a graph with numerically labeled edges (called branches) representing a Coxeter group or...
57 KB (3,217 words) - 14:44, 18 October 2024
reflection group. In fact it turns out that most finite reflection groups are Weyl groups. Abstractly, Weyl groups are finite Coxeter groups, and are important...
21 KB (3,252 words) - 00:45, 7 May 2024
In mathematics, a Coxeter element is an element of an irreducible Coxeter group which is a product of all simple reflections. The product depends on the...
19 KB (1,641 words) - 17:59, 20 November 2024
n Coxeter group has n mirrors and is represented by a Coxeter–Dynkin diagram. Coxeter notation offers a bracketed notation equivalent to the Coxeter diagram...
69 KB (1,170 words) - 05:21, 23 July 2024
Iwahori–Hecke algebra (redirect from Hecke algebra of a Coxeter group)
is a deformation of the group algebra of a Coxeter group. Hecke algebras are quotients of the group rings of Artin braid groups. This connection found...
15 KB (2,078 words) - 18:21, 6 November 2024
geometry and group theory are named after him, including the Coxeter graph, Coxeter groups, Coxeter's loxodromic sequence of tangent circles, Coxeter–Dynkin...
16 KB (1,627 words) - 18:52, 26 October 2024
In group theory, the Todd–Coxeter algorithm, created by J. A. Todd and H. S. M. Coxeter in 1936, is an algorithm for solving the coset enumeration problem...
7 KB (1,168 words) - 13:31, 17 April 2020
context—for example, whether one is discussing general Coxeter groups or complex reflection groups—but in all cases the collection of parabolic subgroups...
28 KB (3,742 words) - 00:35, 1 November 2024
Michael W. Davis (section Coxeter groups)
is the author of two books that include The Geometry and Topology of Coxeter Groups and Multiaxial Actions on Manifolds. His notable contributions to the...
12 KB (1,084 words) - 00:37, 14 November 2024
with Coxeter groups. Examples are free groups, free abelian groups, braid groups, and right-angled Artin–Tits groups, among others. The groups are named...
20 KB (2,995 words) - 00:33, 29 June 2024
Coxeter notation (also Coxeter symbol) is a system of classifying symmetry groups, describing the angles between fundamental reflections of a Coxeter...
175 KB (6,423 words) - 21:15, 29 July 2024
infinite facets whose quotient group of their normal abelian subgroups is finite. They include the one-dimensional Coxeter group I ~ 1 {\displaystyle {\tilde...
22 KB (2,527 words) - 03:23, 10 November 2024
reflection group. Reflection groups also include Weyl groups and crystallographic Coxeter groups. While the orthogonal group is generated by reflections...
7 KB (867 words) - 09:08, 22 September 2024
Bi=M\wr \mathbb {Z} _{2}.\,} The Bimonster is also a quotient of the Coxeter group corresponding to the Dynkin diagram Y555, a Y-shaped graph with 16 nodes:...
6 KB (634 words) - 14:45, 26 April 2024
symmetry of the E8 group. It was discovered by Thorold Gosset, published in his 1900 paper. He called it an 8-ic semi-regular figure. Its Coxeter symbol is 421...
38 KB (2,556 words) - 04:13, 24 July 2024
groups in two dimensions. Other finite subgroups include: Permutation matrices (the Coxeter group An) Signed permutation matrices (the Coxeter group Bn);...
56 KB (7,844 words) - 19:18, 11 October 2024
{A}}_{3}} Coxeter group. This honeycomb has four uniform constructions, with the truncated octahedral cells having different Coxeter groups and Wythoff...
15 KB (871 words) - 06:47, 7 November 2024
mathematics, the Coxeter complex, named after H. S. M. Coxeter, is a geometrical structure (a simplicial complex) associated to a Coxeter group. Coxeter complexes...
7 KB (1,254 words) - 06:48, 20 June 2024
theory of Coxeter groups, the symmetric group is the Coxeter group of type An and occurs as the Weyl group of the general linear group. In combinatorics...
46 KB (6,195 words) - 17:16, 4 November 2024
special kind of Coxeter diagram), the Weyl group (a concrete reflection group), or the abstract Coxeter group. Although the Weyl group is abstractly isomorphic...
77 KB (5,608 words) - 07:05, 10 May 2024
5-cell (section As a Boerdijk–Coxeter helix)
'pentachoron, pentatope, pentahedroid, tetrahedral pyramid, or 4-simplex (Coxeter's α 4 {\displaystyle \alpha _{4}} polytope), the simplest possible convex...
38 KB (3,797 words) - 12:47, 24 September 2024
(7 3 2) triangle group, Coxeter group [7,3], orbifold (*732) contains these uniform tilings: The (8 3 2) triangle group, Coxeter group [8,3], orbifold...
28 KB (1,586 words) - 09:51, 5 October 2024
{\displaystyle {\tilde {A}}_{3}} Coxeter group. The symmetry can be multiplied by the symmetry of rings in the Coxeter–Dynkin diagrams: The rectified cubic...
66 KB (3,191 words) - 03:59, 10 November 2024
passing through the same point are the finite Coxeter groups, represented by Coxeter notation. The point groups in three dimensions are heavily used in chemistry...
60 KB (5,112 words) - 20:34, 5 November 2024
F4 (mathematics) (category Algebraic groups)
Dynkin diagram for F4 is: . Its Weyl/Coxeter group G = W(F4) is the symmetry group of the 24-cell: it is a solvable group of order 1152. It has minimal faithful...
8 KB (983 words) - 13:15, 27 September 2024
four-dimensional crystal classes 1985 H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, Coxeter notation for 4D point groups 2003 John Conway and Smith, On Quaternions...
53 KB (3,559 words) - 07:49, 2 August 2024
x1, x2, x3, x4) with -1 < xi < 1 for all i. n-cube Coxeter plane projections in the Bk Coxeter groups project into k-cube graphs, with power of two vertices...
10 KB (826 words) - 03:51, 20 April 2024
Coxeter notation (rectangular): [∞,2,∞] or [∞]×[∞] Coxeter notation (square): [4,1+,4] or [1+,4,4,1+] Lattice: rectangular Point group: D2 The group pmm...
65 KB (6,483 words) - 19:00, 20 November 2024
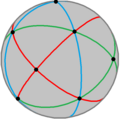
Icosahedral symmetry (redirect from Icosahedral group)
of 120. The full symmetry group is the Coxeter group of type H3. It may be represented by Coxeter notation [5,3] and Coxeter diagram . The set of rotational...
48 KB (2,349 words) - 19:51, 14 September 2024