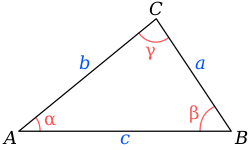
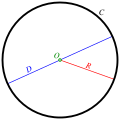
trigonometry, the law of cosines (also known as the cosine formula or cosine rule) relates the lengths of the sides of a triangle to the cosine of one of its angles...
38 KB (5,891 words) - 16:21, 8 June 2025
spherical trigonometry, the law of cosines (also called the cosine rule for sides) is a theorem relating the sides and angles of spherical triangles, analogous...
13 KB (2,181 words) - 13:44, 22 April 2025
Pythagorean theorem (redirect from Pythagoras's Law)
{b}{R}}} where cosh is the hyperbolic cosine. This formula is a special form of the hyperbolic law of cosines that applies to all hyperbolic triangles:...
95 KB (12,787 words) - 21:00, 12 July 2025
the cosine of the angle θ between the observer's line of sight and the surface normal; I = I0 cos θ. The law is also known as the cosine emission law or...
9 KB (1,279 words) - 21:47, 17 February 2025
the "law of cosines" is a pair of theorems relating the sides and angles of triangles on a hyperbolic plane, analogous to the planar law of cosines from...
12 KB (1,686 words) - 10:57, 11 May 2024
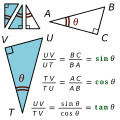
Trigonometry (section Law of cosines)
{(a+b+c)(a-b+c)(a+b-c)(b+c-a)}}}.} The law of cosines (known as the cosine formula, or the "cos rule") is an extension of the Pythagorean theorem to arbitrary...
50 KB (4,947 words) - 14:48, 12 July 2025
being the law of cosines. The law of sines can be generalized to higher dimensions on surfaces with constant curvature. With the side of length a as the...
28 KB (4,303 words) - 15:04, 9 May 2025
Haversine formula (redirect from Law of haversines)
written using cosines (sometimes called the spherical law of cosines, not to be confused with the law of cosines for plane geometry) instead of haversines...
20 KB (2,836 words) - 23:39, 27 May 2025
Trigonometric functions (redirect from Sine-cosine-tangent)
accessible enclosed distance. The law of cosines (also known as the cosine formula or cosine rule) is an extension of the Pythagorean theorem: c 2 = a...
77 KB (10,653 words) - 18:24, 2 July 2025
{\displaystyle \gamma } the angles opposite those sides. Applying the law of cosines we get cos γ = a 2 + b 2 − c 2 2 a b {\displaystyle \cos \gamma ={\frac...
24 KB (3,877 words) - 05:05, 2 July 2025
+\beta )}}.} The law of tangents, although not as commonly known as the law of sines or the law of cosines, is equivalent to the law of sines, and can be...
7 KB (1,179 words) - 20:59, 19 June 2025
Dot product (redirect from Generalizations of the dot product)
\\\end{aligned}}} which is the law of cosines. There are two ternary operations involving dot product and cross product. The scalar triple product of three vectors is...
28 KB (4,426 words) - 07:56, 22 June 2025
Jamshid al-Kashi (section Law of cosines)
law of cosines is sometimes referred to as the théorème d'Al-Kashi. In discussing decimal fractions, Struik states that (p. 7): "The introduction of decimal...
25 KB (2,999 words) - 08:16, 9 June 2025
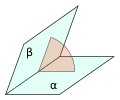
Dihedral angle (redirect from Angle of planes)
)\sin(\angle \mathrm {BPC} )}}} This can be deduced from the spherical law of cosines, but can also be found by other means. In m-dimensional Euclidean space...
14 KB (2,106 words) - 19:58, 18 June 2025
two proofs of the cosine rule (Articles 37 and 60) and two proofs of the sine rule (Articles 40 and 42). The page on Spherical law of cosines gives four...
40 KB (6,765 words) - 14:04, 8 July 2025
Hinge theorem (section Proof from the law of cosines)
Book I of Euclid's Elements. The theorem is an immediate corollary of the law of cosines. For two triangles with sides { a , b , c } {\displaystyle \{a,b...
3 KB (445 words) - 23:44, 9 May 2025
equal either 30° or 150°. Using the law of cosines avoids this problem: within the interval from 0° to 180° the cosine value unambiguously determines its...
23 KB (3,698 words) - 09:43, 25 October 2024
consequence of – another existing theorem. The 'Porism' can be viewed on pages 36 and 37 of DROC (Harvard electronic copy) "Sine, Cosine, and Ptolemy's...
28 KB (5,051 words) - 22:17, 19 April 2025
Tetrahedron (section Law of cosines for tetrahedra)
faces of the tetrahedron adjacent to the edge P i P j {\displaystyle P_{i}P_{j}} . The law of cosines for a tetrahedron, which relates the areas of the...
75 KB (9,514 words) - 16:26, 14 July 2025
tetrahedra is 5-dimensional. See: Law of sines The law of cosines for the tetrahedron relates the areas of each face of the tetrahedron and the dihedral...
12 KB (3,048 words) - 02:08, 20 July 2024
the polarization of an algebraic form. Inner product space – Vector space with generalized dot product Law of cosines – Generalization of Pythagorean theorem...
26 KB (4,506 words) - 22:05, 19 June 2025
law. In the parallelogram on the right, let AD = BC = a, AB = DC = b, ∠ B A D = α . {\displaystyle \angle BAD=\alpha .} By using the law of cosines in...
9 KB (1,633 words) - 00:18, 20 June 2025
proved using vectors (see parallelogram law). The following is an independent proof using the law of cosines. Let the triangle have sides a , b , c {\displaystyle...
7 KB (776 words) - 09:17, 27 March 2025
the Earth, the cosine of the central angle is near 0.99999999). For modern 64-bit floating-point numbers, the spherical law of cosines formula, given...
13 KB (1,920 words) - 08:30, 23 January 2025
circumradius. The law of cosines is useful for computing the length of an unknown side if two other sides and an angle are known. The law states, a 2 + b...
55 KB (7,064 words) - 00:33, 30 May 2025
the law of cosines for sides reduces to the planar law of cosines and two of Napier's analogies reduce to Mollweide's formulas above. But the law of cosines...
9 KB (1,757 words) - 09:24, 23 December 2024
specific trigonometric laws or formulas. For instance, propositions twelve and thirteen of book two of the Elements are the laws of cosines for obtuse and acute...
53 KB (6,835 words) - 05:32, 11 June 2025
triangle inequality is a consequence of the Pythagorean theorem, and for general triangles, a consequence of the law of cosines, although it may be proved without...
35 KB (5,287 words) - 10:38, 18 June 2025
)^{3}{\textrm {d}}\theta .} Here s(θ) can be found in terms of q and θ using the Law of cosines. The steps needed to evaluate the integral, together with...
10 KB (1,674 words) - 23:58, 28 March 2025
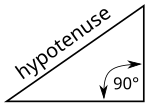
Hypotenuse (category Parts of a triangle)
angle γ (gamma), where the adjacent leg equals 0, the cosine of γ also equals 0. The law of cosines formulates that c 2 = a 2 + b 2 − 2 a b cos θ {\displaystyle...
10 KB (1,311 words) - 17:07, 12 June 2025