the term "Banach space" and Banach in turn then coined the term "Fréchet space" to mean a complete metrizable topological vector space, without the local...

metrizable (resp. pseudometrizable) topological vector space (TVS) is a TVS whose topology is induced by a metric (resp. pseudometric). An LM-space is...

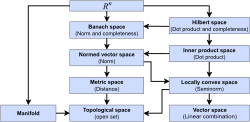
In mathematics, a topological vector space (also called a linear topological space and commonly abbreviated TVS or t.v.s.) is one of the basic structures...

areas of mathematics, a metrizable space is a topological space that is homeomorphic to a metric space. That is, a topological space ( X , τ ) {\displaystyle...

convex topological vector spaces that are completely metrizable (with a choice of complete metric). They are generalizations of Banach spaces, which are...

analysis and related areas of mathematics, a complete topological vector space is a topological vector space (TVS) with the property that whenever points get...

put it more abstractly every seminormed vector space is a topological vector space and thus carries a topological structure which is induced by the semi-norm...

(functional analysis) LB-space LF-space – Topological vector space Metrizable topological vector space – A topological vector space whose topology can be defined...

Conversely, not every topological space can be given a metric. Topological spaces which are compatible with a metric are called metrizable and are particularly...

if it is complete as a topological vector space. If ( X , τ ) {\displaystyle (X,\tau )} is a metrizable topological vector space (such as any norm induced...

In mathematics, a completely metrizable space (metrically topologically complete space) is a topological space (X, T) for which there exists at least...

Kolmogorov in 1935. Suppose X {\displaystyle X} is a topological vector space (TVS) over a topological field K . {\displaystyle \mathbb {K} .} A subset B...

topology of local convergence in measure is an F-space, i.e. a completely metrizable topological vector space. Moreover, this topology is isometric to global...

mathematics, a barrelled space (also written barreled space) is a topological vector space (TVS) for which every barrelled set in the space is a neighbourhood...

} Metrizable topological vector space – A topological vector space whose topology can be defined by a metric Norm (mathematics) – Length in a vector space...

and related areas of mathematics, a topological property or topological invariant is a property of a topological space that is invariant under homeomorphisms...

category theorem is purely topological, it applies to these spaces as well. Completely metrizable spaces are often called topologically complete. However, the...

for a topological space to be a Baire space. (BCT1) Every complete pseudometric space is a Baire space. In particular, every completely metrizable topological...

In mathematics, topological groups are the combination of groups and topological spaces, i.e. they are groups and topological spaces at the same time,...

a locally convex metrizable topological vector space is a neighborhood of the origin. Closed vector subspaces of bornological space need not be bornological...

of a paracompact space and a compact space is always paracompact. Every metric space is paracompact. A topological space is metrizable if and only if it...

}} ⁠ is Fréchet, meaning that it is a complete, metrizable, locally convex topological vector space (TVS). However, this topology is rather pathological:...

a continuous linear transformation between topological vector spaces. An operator between two normed spaces is a bounded linear operator if and only if...

mathematics, a normal space is a topological space in which any two disjoint closed sets have disjoint open neighborhoods. Such spaces need not be Hausdorff...

metric tensor Metric space – Mathematical space with a notion of distance Metrizable topological vector space – A topological vector space whose topology can...

mathematics, particularly in functional analysis, a Mackey space is a locally convex topological vector space X such that the topology of X coincides with the Mackey...

complete metrizable topological vector space X {\displaystyle X} (such as a Fréchet space or an F-space) into a Hausdorff topological vector space Y . {\displaystyle...

agree in a metric space, but may not be equivalent in other topological spaces. One such generalization is that a topological space is sequentially compact...

continuous function. Every topological group G {\displaystyle G} (in particular, every topological vector space) becomes a uniform space if we define a subset...

topological vector space is locally convex if and only if its topology is induced by a family of seminorms. Let X {\displaystyle X} be a vector space...