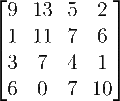In linear algebra, the Cayley–Hamilton theorem (named after the mathematicians Arthur Cayley and William Rowan Hamilton) states that every square matrix...

Cambridge for 35 years. He postulated what is now known as the Cayley–Hamilton theorem—that every square matrix is a root of its own characteristic polynomial...

clearly the characteristic polynomial of the Jordan form of A. The Cayley–Hamilton theorem asserts that every matrix A satisfies its characteristic equation:...

R[s,t].} Multiply sI − A by its adjugate. Since p(A) = 0 by the Cayley–Hamilton theorem, some elementary manipulations reveal adj ⁡ ( s I − A ) = Δ p (...

Cayley graph of a finite Coxeter group is Hamiltonian (For more information on Hamiltonian paths in Cayley graphs, see the Lovász conjecture.) Cayley...

known as Padé approximants), and gave the first full proof for the Cayley–Hamilton theorem. He also lent his name to certain differential-geometric objects...

{tr} A^{k-1}&&\cdots &\operatorname {tr} A\end{vmatrix}}~.} The Cayley–Hamilton theorem states that replacing t {\displaystyle t} by A {\displaystyle A}...

Hamilton's principle, Hamilton's principal function, the Hamilton–Jacobi equation, Cayley-Hamilton theorem are named after Hamilton. The Hamiltonian is...

Cayley graph Cayley numbers Cayley plane Cayley table Cayley transform Cayleyan Cayley–Bacharach theorem Cayley–Dickson construction Cayley–Hamilton theorem...

the lemma is a simple consequence of a generalized form of the Cayley–Hamilton theorem, an observation made by Michael Atiyah (1969). The special case...

Many theorems were first established for small matrices only, for example, the Cayley–Hamilton theorem was proved for 2×2 matrices by Cayley in the...

main ingredients for the following proof are the Cayley–Hamilton theorem and the fundamental theorem of algebra. Let D be the division algebra in question...

{\pi }{6}}\right)^{12}&=N+P=I\\\end{aligned}}} By virtue of the Cayley–Hamilton theorem the matrix exponential is expressible as a polynomial of order...

equation, as its roots are exactly the eigenvalues of A. By the Cayley–Hamilton theorem, A itself obeys the same equation: pA(A) = 0. As a consequence...

linear transformations represented as matrices, most notably the Cayley–Hamilton theorem. The characteristic polynomial of a matrix A is a scalar-valued...

polynomial is the multiple of the minimal polynomial of an operator A. Cayley–Hamilton theorem Minimal polynomial (linear algebra) Taboga, Marco. "Minimal Polynomial"...

characteristic polynomial, which is one way of formulating the Cayley–Hamilton theorem (for the case of matrices over a field). Given an endomorphism...

matrices are nilpotent of index at most n as a consequence of the Cayley-Hamilton theorem. An atomic (upper or lower) triangular matrix is a special form...

determinant trick (that is a variant of the Cayley–Hamilton theorem and yields Nakayama's lemma): Theorem — Let u be an endomorphism of an A-module N...

contaminated by small errors due to imperfect computer arithmetic. The Cayley–Hamilton theorem allows the inverse of A to be expressed in terms of det(A), traces...

divides the characteristic polynomial (which is essentially the Cayley-Hamilton theorem), and that every irreducible factor of the characteristic polynomial...

Cauchy's theorem (finite groups) Cayley–Bacharach theorem (projective geometry) Cayley–Hamilton theorem (Linear algebra) Cayley–Salmon theorem (algebraic...

the characteristic polynomial, and explicit applications of the Cayley–Hamilton theorem. For example, starting from the following equation, which was proved...

Characteristic polynomial Trace Eigenvalue, eigenvector and eigenspace Cayley–Hamilton theorem Spread of a matrix Jordan normal form Weyr canonical form Rank...

the Cayley–Dickson construction takes any algebra with involution to another algebra with involution of twice the dimension.: 45  Hurwitz's theorem (composition...

function for the Wahba's problem as a quadratic form, using the Cayley–Hamilton theorem and the Newton–Raphson method to efficiently solve the eigenvalue...

after William Rowan Hamilton: Cayley–Hamilton theorem Hamilton's equations Hamilton's principle Hamilton–Jacobi equation Hamilton–Jacobi–Bellman equation...

_{1i}x+\cdots +\beta _{(n-1)i}x^{n-1}.} Frobenius endomorphism Cayley–Hamilton theorem Krylov subspace Horn, Roger A.; Charles R. Johnson (1985). Matrix...

be complex even if the entries of A are real. According to the Cayley–Hamilton theorem, pA(A) = 0, that is, the result of substituting the matrix itself...

A ) = 0 {\displaystyle p(A)=0} due to the Cayley–Hamilton theorem; meanwhile, the spectral mapping theorem tells us σ ( p ( − B ) ) = p ( σ ( − B ) )...