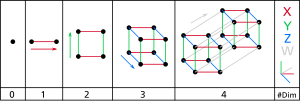In mathematics and physics, a vector space (also called a linear space) is a set whose elements, often called vectors, can be added together and multiplied...

In mathematics, the dimension of a vector space V is the cardinality (i.e., the number of vectors) of a basis of V over its base field. It is sometimes...

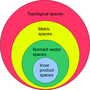
A topological vector space is a vector space that is also a topological space with the property that the vector space operations (vector addition and scalar...

In mathematics, a normed vector space or normed space is a vector space over the real or complex numbers on which a norm is defined. A norm is a generalization...

In mathematics, a set B of vectors in a vector space V is called a basis (pl.: bases) if every element of V may be written in a unique way as a finite...

Vector space model or term vector model is an algebraic model for representing text documents (or more generally, items) as vectors such that the distance...

mathematics, an inner product space (or, rarely, a Hausdorff pre-Hilbert space) is a real vector space or a complex vector space with an operation called an...

This page lists some examples of vector spaces. See vector space for the definitions of terms used on this page. See also: dimension, basis. Notation...

a graded vector space is a vector space that has the extra structure of a grading or gradation, which is a decomposition of the vector space into a direct...

In mathematics, a super vector space is a Z 2 {\displaystyle \mathbb {Z} _{2}} -graded vector space, that is, a vector space over a field K {\displaystyle...

In mathematics, a symplectic vector space is a vector space V {\displaystyle V} over a field F {\displaystyle F} (for example the real numbers R {\displaystyle...

In mathematics, a norm is a function from a real or complex vector space to the non-negative real numbers that behaves in certain ways like the distance...

The orientation of a real vector space or simply orientation of a vector space is the arbitrary choice of which ordered bases are "positively" oriented...

In mathematics, any vector space V {\displaystyle V} has a corresponding dual vector space (or just dual space for short) consisting of all linear forms...

on the above sorts of vectors. A vector space formed by geometric vectors is called a Euclidean vector space, and a vector space formed by tuples is called...

functional analysis, a Banach space (pronounced [ˈbanax]) is a complete normed vector space. Thus, a Banach space is a vector space with a metric that allows...

re-formalized to define Euclidean spaces through axiomatic theory. Another definition of Euclidean spaces by means of vector spaces and linear algebra has been...

transformation, vector space homomorphism, or in some contexts linear function) is a mapping V → W {\displaystyle V\to W} between two vector spaces that preserves...

topological vector spaces (LCTVS) or locally convex spaces are examples of topological vector spaces (TVS) that generalize normed spaces. They can be...

point, the zero vector is called the origin. Adding a fixed vector to the elements of a linear subspace (vector subspace) of a vector space produces an affine...

mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X {\displaystyle...

Fréchet spaces, named after Maurice Fréchet, are special topological vector spaces. They are generalizations of Banach spaces (normed vector spaces that...

mathematics, the complex conjugate of a complex vector space V {\displaystyle V\,} is a complex vector space V ¯ {\displaystyle {\overline {V}}} that has...

In mathematics, the dimension theorem for vector spaces states that all bases of a vector space have equally many elements. This number of elements may...

vector space V {\displaystyle V} by a subspace N {\displaystyle N} is a vector space obtained by "collapsing" N {\displaystyle N} to zero. The space obtained...

(some authors use VectK) has all vector spaces over a field K as objects, and K-linear maps as morphisms. Since vector spaces over K (as a field) are the same...

linear hull or just span) of a set S {\displaystyle S} of elements of a vector space V {\displaystyle V} is the smallest linear subspace of V {\displaystyle...

Vector Space Model (TVSM) (literature: [1]) extends the vector space model of information retrieval by removing the constraint that the term-vectors be...

theory of vector spaces, a set of vectors is said to be linearly independent if there exists no nontrivial linear combination of the vectors that equals...

analytic geometry. In condensed mathematics, liquid vector spaces are alternatives to topological vector spaces. A condensed set is a sheaf of sets on the site...