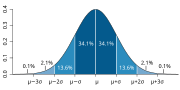
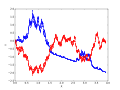
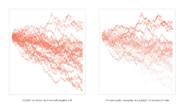
mathematics, the Wiener process is a real-valued continuous-time stochastic process named in honor of American mathematician Norbert Wiener for his investigations...

probability for stochastic processes, the reflection principle for a Wiener process states that if the path of a Wiener process f(t) reaches a value f(s)...

stochastic processes. Examples of such stochastic processes include the Wiener process or Brownian motion process, used by Louis Bachelier to study price changes...

sports club in Vienna Wiener process, a mathematical model related to Brownian motion Wiener equation, named after Norbert Wiener, assumes the current...

such a process is called mean-reverting. The process can be considered to be a modification of the random walk in continuous time, or Wiener process, in...

Technology (MIT). A child prodigy, Wiener later became an early researcher in stochastic and mathematical noise processes, contributing work relevant to electronic...

motion (the Wiener process). The best known of these is attributed to Paul Lévy (1939). All three laws relate path properties of the Wiener process to the...

In signal processing, the Wiener filter is a filter used to produce an estimate of a desired or target random process by linear time-invariant (LTI) filtering...

extends the methods of calculus to stochastic processes such as Brownian motion (see Wiener process). It has important applications in mathematical...

Lawler, Schramm and Werner. A Wiener process enjoys many symmetries a random walk does not. For example, a Wiener process walk is invariant to rotations...

theorem first for the special case when the underlying stochastic process is a Wiener process. This special case is sufficient for risk-neutral pricing in...

Predictable process, a stochastic process whose value is knowable Stochastic process, a random process, as opposed to a deterministic process Wiener process, a...

In statistics, a generalized Wiener process (named after Norbert Wiener) is a continuous time random walk with drift and random jumps at every point in...

Lévy process may thus be viewed as the continuous-time analog of a random walk. The most well known examples of Lévy processes are the Wiener process, often...

best-known stochastic process to which stochastic calculus is applied is the Wiener process (named in honor of Norbert Wiener), which is used for modeling...

Gaussian process whose covariance function is a generalisation of that of the Wiener process. Let f {\displaystyle f} be a mean-zero Gaussian process { X t...

statistics, diffusion processes are a class of continuous-time Markov process with almost surely continuous sample paths. Diffusion process is stochastic in...

important examples of Markov processes are the Wiener process, also known as the Brownian motion process, and the Poisson process, which are considered the...

Wiener process. Property (3) means that every non-degenerate mean-square continuous Gauss–Markov process can be synthesized from the standard Wiener process...

wide-sense-stationary random process has a spectral decomposition given by the power spectral density of that process. Norbert Wiener proved this theorem for...

set of Wiener processes alone), any equivalent measure can be described in a very loose sense by adding a drift to each of the Wiener processes. By selecting...

continuous-time gaussian process B(t) whose probability distribution is the conditional probability distribution of a standard Wiener process W(t) (a mathematical...

statistics, econometrics, and signal processing, an autoregressive (AR) model is a representation of a type of random process; as such, it can be used to describe...

filter Wiener's lemma Wiener process Generalized Wiener process Wiener sausage Wiener series Wiener–Hopf method Wiener–Ikehara theorem Wiener–Khinchin...

(usually n-dimensional Euclidean space). Classical Wiener space is useful in the study of stochastic processes whose sample paths are continuous functions....

be a stochastic process that is adapted to the natural filtration F ∗ W {\displaystyle {\mathcal {F}}_{*}^{W}} of the Wiener process.[clarification needed]...

The Wiener sausage was named after Norbert Wiener by M. D. Donsker and S. R. Srinivasa Varadhan (1975) because of its relation to the Wiener process; the...

described by the Wiener process, a continuous-time stochastic process named in honor of Norbert Wiener. It is one of the best known Lévy processes (càdlàg stochastic...

Nikolay Krylov. In one spatial dimension x, for an Itô process driven by the standard Wiener process W t {\displaystyle W_{t}} and described by the stochastic...

terms up to first order in the time increment and second order in the Wiener process increment. The lemma is widely employed in mathematical finance, and...