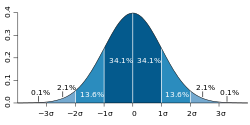
In probability theory, Chebyshev's inequality (also called the Bienaymé–Chebyshev inequality) provides an upper bound on the probability of deviation...

first Chebyshev inequality, while referring to Chebyshev's inequality as the second Chebyshev inequality) or Bienaymé's inequality. Markov's inequality (and...

probability theory, the multidimensional Chebyshev's inequality is a generalization of Chebyshev's inequality, which puts a bound on the probability of...

Cantelli's inequality (also called the Chebyshev-Cantelli inequality and the one-sided Chebyshev inequality) is an improved version of Chebyshev's inequality for...

In mathematics, Chebyshev's sum inequality, named after Pafnuty Chebyshev, states that if a 1 ≥ a 2 ≥ ⋯ ≥ a n {\displaystyle a_{1}\geq a_{2}\geq \cdots...

between n and 2n. Chebyshev's inequality, on the range of standard deviations around the mean, in statistics Chebyshev's sum inequality, about sums and...

several more general laws of large numbers in probability theory. Chebyshev's inequality. Let X be a random variable with finite expected value μ and finite...

Accuracy and precision Algorithms for calculating variance Chebyshev's inequality An inequality on location and scale parameters Coefficient of variation...

Markov's inequality or Chebyshev's inequality. The Chernoff bound is related to the Bernstein inequalities. It is also used to prove Hoeffding's inequality, Bennett's...

the Chebyshev inequality (which can be used to prove the weak law of large numbers), the Bertrand–Chebyshev theorem, Chebyshev polynomials, Chebyshev linkage...

and Chebyshev inequalities often give much weaker information than is otherwise available. For example, in the case of an unweighted dice, Chebyshev's inequality...

deviation of X {\displaystyle X} . Chebyshev's inequality can be seen as a special case of the generalized Markov's inequality applied to the random variable...

polynomials Chebyshev filter Chebyshev's inequality Chebyshev distance Chebyshev (crater): A lunar crater 2010 Chebyshev: An asteroid from the asteroid...

inequality Chebyshev–Markov–Stieltjes inequalities Chebyshev's sum inequality Clarkson's inequalities Eilenberg's inequality Fekete–Szegő inequality Fenchel's...

Azuma's inequality Bernoulli's inequality Bell's inequality Boole's inequality Cauchy–Schwarz inequality Chebyshev's inequality Chernoff's inequality Cramér–Rao...

Concentration inequality - a summary of tail-bounds on random variables. Hoeffding's inequality S.N.Bernstein, "On a modification of Chebyshev's inequality and...

inequality follows by Chebyshev's inequality. This inequality was generalized by Hájek and Rényi in 1955. Chebyshev's inequality Etemadi's inequality...

Vysochanskiï–Petunin inequality, a similar result for the distance from the mean rather than the mode Chebyshev's inequality, concerns distance from...

qualify as a discovery. A weaker three-sigma rule can be derived from Chebyshev's inequality, stating that even for non-normally distributed variables, at least...

{n-1}{\sqrt {n}}}.} Chebyshev's inequality locates a certain fraction of the data within certain bounds, while Samuelson's inequality locates all the data...

модификациях неравенства Чебышёва [On certain modifications of Chebyshev's inequality]. Doklady Akademii Nauk SSSR (in Russian). 17 (6): 275–277. (vol...

second is the Vysochanskiï–Petunin inequality, a refinement of the Chebyshev inequality. The Chebyshev inequality guarantees that in any probability distribution...

inequalities Chebyshev's bias Chebyshev's inequality in probability and statistics Chebyshev–Cantelli inequality Multidimensional Chebyshev's inequality...

95% confidence)[citation needed]. Cantelli's inequality is the one-tailed version of Chebyshev's inequality. Binomial proportion confidence interval Rule...

relation holds uniformly in x, which can be seen from its proof via Chebyshev's inequality, taking into account that the variance of 1⁄n K, equal to 1⁄n x(1−x)...

information that a variance does not. For inequalities associated with the semivariance, see Chebyshev's inequality § Semivariances. The term variance was...

Mathematics portal Chebyshev rational functions Function approximation Discrete Chebyshev transform Markov brothers' inequality Rivlin, Theodore J. (1974)...

unimodality Chebyshev's inequality would give a looser bound of 1/9 = 0.11111.... An improved version of the Vysochanskij-Petunin inequality for one-sided...

(in which case it is known as Markov inequality), or the quadratic function (respectively Chebyshev's inequality). Another useful result is the continuous...

geometric mean inequality, the Cauchy–Schwarz inequality, and Chebyshev's sum inequality. As a simple example, consider real numbers x 1 ≤ ⋯ ≤ x n {\displaystyle...