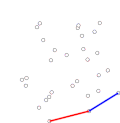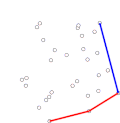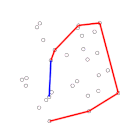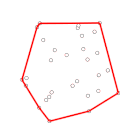
In geometry, the convex hull, convex envelope or convex closure of a shape is the smallest convex set that contains it. The convex hull may be defined either...

Algorithms that construct convex hulls of various objects have a broad range of applications in mathematics and computer science. In computational geometry...

"balanced"), in which case it is called a disk. The disked hull or the absolute convex hull of a set is the intersection of all disks containing that set...

is always a convex curve. The intersection of all the convex sets that contain a given subset A of Euclidean space is called the convex hull of A. It is...

locally convex space, the convex hull and the disked hull of a totally bounded set is totally bounded. In a complete locally convex space, the convex hull and...

Carathéodory's theorem is a theorem in convex geometry. It states that if a point x {\displaystyle x} lies in the convex hull C o n v ( P ) {\displaystyle \mathrm...

The polynomially convex hull contains the holomorphically convex hull. The domain G {\displaystyle G} is called holomorphically convex if for every compact...

or vertices. A convex polyhedron is a polyhedron that bounds a convex set. Every convex polyhedron can be constructed as the convex hull of its vertices...

learning resources about Convex combination Affine hull Carathéodory's theorem (convex hull) Simplex Barycentric coordinate system Convex space Rockafellar,...

every convex set is orthogonally convex but not vice versa. For the same reason, the orthogonal convex hull itself is a subset of the convex hull of the...

geometry Conical hull, in convex geometry Convex hull, in convex geometry Carathéodory's theorem (convex hull) Holomorphically convex hull, in complex analysis...

convex set of points in space. Other important definitions are: as the intersection of half-spaces (half-space representation) and as the convex hull...

The dynamic convex hull problem is a class of dynamic problems in computational geometry. The problem consists in the maintenance, i.e., keeping track...

Closed hulls In a locally convex space, convex hulls of bounded sets are bounded. This is not true for TVSs in general. The closed convex hull of a set...

the convex hull of its edges. Additional properties of convex polygons include: The intersection of two convex polygons is a convex polygon. A convex polygon...

Local convex hull (LoCoH) is a method for estimating size of the home range of an animal or a group of animals (e.g. a pack of wolves, a pride of lions...

and computational geometry, the relative convex hull or geodesic convex hull is an analogue of the convex hull for the points inside a simple polygon or...

Delone triangulation of a set of points in the plane subdivides their convex hull into triangles whose circumcircles do not contain any of the points....

A kinetic convex hull data structure is a kinetic data structure that maintains the convex hull of a set of continuously moving points. It should be distinguished...

to the closed convex hull of its extreme points. This theorem generalizes to infinite-dimensional spaces and to arbitrary compact convex sets the following...

geometric object that was discovered by Paul Schatz in 1929. It is the convex hull of a skeletal frame made by placing two linked congruent circles in perpendicular...

Graham's scan is a method of finding the convex hull of a finite set of points in the plane with time complexity O(n log n). It is named after Ronald...

In discrete geometry and computational geometry, the convex hull of a simple polygon is the polygon of minimum perimeter that contains a given simple...

piece from a figure, its area decreases but its perimeter may not. The convex hull of a figure may be visualized as the shape formed by a rubber band stretched...

on convex sets, published by Johann Radon in 1921, states that: Any set of d + 2 points in Rd can be partitioned into two sets whose convex hulls intersect...

encoding of the convex hull of the function's epigraph in terms of its supporting hyperplanes. For more examples, see § Table of selected convex conjugates...

geometry, the gift wrapping algorithm is an algorithm for computing the convex hull of a given set of points. In the two-dimensional case the algorithm is...

spheres determines a specific volume known as the convex hull of the packing, defined as the smallest convex set that includes all the spheres. There are many...

balanced hull of a convex set may fail to be convex (however, the convex hull of a balanced set is always balanced). For an example, let the convex subset...

S_{2}} of a real vector space, the convex hull of their Minkowski sum is the Minkowski sum of their convex hulls: Conv ⁡ ( S 1 + S 2 ) = Conv ⁡ ( S 1...