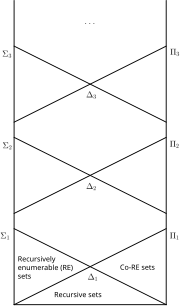
called arithmetical. The arithmetical hierarchy was invented independently by Kleene (1943) and Mostowski (1946). The arithmetical hierarchy is important...

descriptive set theory, the analytical hierarchy is an extension of the arithmetical hierarchy. The analytical hierarchy of formulas includes formulas in the...

called "arithmetical". More formally, the arithmetical hierarchy assigns classifications to the formulas in the language of first-order arithmetic. The classifications...

an arithmetical number that is not computable. The definitions of arithmetical and analytical reals can be stratified into the arithmetical hierarchy and...

and the arithmetical hierarchy, which is a classification of certain subsets of the natural numbers based on their definability in arithmetic. Much recent...

counterpart to the arithmetical hierarchy and analytical hierarchy from mathematical logic. The union of the classes in the hierarchy is denoted PH. Classes...

theorem, named after Emil Post, describes the connection between the arithmetical hierarchy and the Turing degrees. The statement of Post's theorem uses several...

arithmetical set (or arithmetic set) is a set of natural numbers that can be defined by a formula of first-order Peano arithmetic. The arithmetical sets...

using the arithmetical hierarchy and analytical hierarchy. The higher-order counterparts of the major subsystems of second-order arithmetic generally...

provide many examples of sets which are complete at some level of the arithmetical hierarchy. Here, we say a Σ n {\displaystyle \Sigma _{n}} set A {\displaystyle...

variables (that is, no quantifiers over set variables) is called arithmetical. An arithmetical formula may have free set variables and bound individual variables...

Borel hierarchy extends the arithmetical hierarchy of subsets of an effective Polish space. It is closely related to the hyperarithmetical hierarchy. The...

formal semantics. Informally, the theorem states that "arithmetical truth cannot be defined in arithmetic". The theorem applies more generally to any sufficiently...

computability, the T predicate can be used to generate complete sets in the arithmetical hierarchy. In particular, the set K = { e   :   ∃ x T 1 ( e , 0 , x ) } {\displaystyle...

. Iteration of limit computability can be used to climb up the arithmetical hierarchy. Namely, an m {\displaystyle m} -ary function f ( x 1 , … , x m...

set S is Σ 1 0 {\displaystyle \Sigma _{1}^{0}} (referring to the arithmetical hierarchy). There is a partial computable function f such that: f ( x ) =...

or lower in the arithmetical hierarchy. Post's theorem shows that, for each n, Thn( N {\displaystyle {\mathcal {N}}} ) is arithmetically definable, but...

are more expressive, and define sets in the higher levels of the arithmetical hierarchy. Although the usual natural numbers satisfy the axioms of PA, there...

sets of complexity Σ 1 0 {\displaystyle \Sigma _{1}^{0}} in the arithmetical hierarchy, the same as the standard halting problem. The variants are thus...

the arithmetical hierarchy classifies computable, partial functions. Moreover, this hierarchy is strict such that at any other class in the arithmetic hierarchy...

establishes a relationship between the Turing jump operator and the arithmetical hierarchy of sets of natural numbers. Informally, given a problem, the Turing...

all arithmetical formulas, Γ-soundness is called just (arithmetical) soundness. If the language of T consists only of the language of arithmetic (as opposed...

levels of the arithmetical hierarchy, this means that Δ 2 0 {\displaystyle \Delta _{2}^{0}} is the lowest level in the arithmetical hierarchy where random...

terms Π0 n, a set in the arithmetical hierarchy Π1 n, a set in the analytical hierarchy ΠP i, a set in the polynomial hierarchy Π(x) (Pi function), the...

equations involving analytic functions Analytical hierarchy, an extension of the arithmetical hierarchy Analytic set, the continuous image of a Polish space...

elementary, context-sensitive, and primitive recursive. In the arithmetical hierarchy, an arithmetical formula that contains only bounded quantifiers is called...

with its complement co-RE, correspond to the first level of the arithmetical hierarchy. The set of halting Turing machines is recursively enumerable but...

In computing, an arithmetic logic unit (ALU) is a combinational digital circuit that performs arithmetic and bitwise operations on integer binary numbers...

is analogous to the arithmetical hierarchy, which provides a similar classification for sentences of the language of arithmetic. In the language of set...

its proof, is an arithmetical relation between two numbers. Therefore, there is a statement form Bew(y) that uses this arithmetical relation to state...