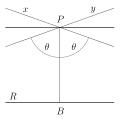
global hyperbolicity is a certain condition on the causal structure of a spacetime manifold (that is, a Lorentzian manifold). It is called hyperbolic...

manifolds. Causality conditions Globally hyperbolic manifold Hyperbolic partial differential equation Orientable manifold Spacetime The Clockwork Rocket...

continuous Causally simple Globally hyperbolic Given are the definitions of these causality conditions for a Lorentzian manifold ( M , g ) {\displaystyle...

Riemannian manifold. Ricci-flat manifolds are a special kind of Einstein manifold. In theoretical physics, Ricci-flat Lorentzian manifolds are of fundamental...

Cauchy surface Closed timelike curve Cosmic censorship hypothesis Globally hyperbolic manifold Malament–Hogarth spacetime Null infinity Penrose diagram Penrose–Hawking...

depend on the choice of the unit vector X {\displaystyle X} . The manifold is called globally Osserman if the spectrum depends neither on X {\displaystyle...

gave rise to hyperbolic geometry and elliptic geometry. In the modern theory of manifolds, these notions correspond to Riemannian manifolds with constant...

model Constructions in hyperbolic geometry Hjelmslev transformation Hyperbolic 3-manifold Hyperbolic manifold Hyperbolic set Hyperbolic tree Kleinian group...

terms, a differentiable manifold is a topological manifold with a globally defined differential structure. Any topological manifold can be given a differential...

equations, the stable manifold theorem is an important result about the structure of the set of orbits approaching a given hyperbolic fixed point. It roughly...

In mathematics and especially differential geometry, a Kähler manifold is a manifold with three mutually compatible structures: a complex structure, a...

geometry of smooth shapes and smooth spaces, otherwise known as smooth manifolds. It uses the techniques of single variable calculus, vector calculus,...

function-theoretic classification but it is hyperbolic in the geometric classification. Dessin d'enfant Kähler manifold Lorentz surface Mapping class group Serre...

infinitely extended saddle shape. There are a great variety of hyperbolic 3-manifolds, and their classification is not completely understood. Those of...

Green’s functions of Lorentzian Green hyperbolic 2nd order partial differential equations in a globally hyperbolic manifold, and in the definition of Hadamard...

0). Hyperbolic rotation of the plane does not mingle the quadrants, in fact, each one is an invariant set under the unit hyperbola group. 4-manifold Clifford-Klein...

orientable Riemannian 2-manifolds into elliptic/parabolic/hyperbolic cases. Each such manifold has a conformally equivalent Riemannian metric with constant...

manifolds of the dynamical system; they behave physically under small perturbations; and they explain many of the observed statistics of hyperbolic systems...

of Three-Manifolds. Princeton University lecture notes. Thurston, William (1982). "Three-dimensional manifolds, Kleinian groups and hyperbolic geometry"...

development is called a globally hyperbolic vacuum development. Choquet-Bruhat also proved a uniqueness theorem: Given any two globally hyperbolic vacuum developments...

feature space or embedding space, is an embedding of a set of items within a manifold in which items resembling each other are positioned closer to one another...

metric space Completion Complex hyperbolic space Conformal map is a map which preserves angles. Conformally flat a manifold M is conformally flat if it is...

globally hyperbolic manifold X = R × M {\displaystyle X=\mathbb {R} \times M} . Since any oriented three-dimensional manifold is parallelizable, a globally hyperbolic...

referred to as hyperbolic LCSs, as they provide a finite-time generalization of the classic concept of normally hyperbolic invariant manifolds in dynamical...

a pseudo-Riemannian manifold. On a Riemannian manifold it is an elliptic operator, while on a Lorentzian manifold it is hyperbolic. The Laplace–de Rham...

Thurston in his influential 1982 paper Three-dimensional manifolds, Kleinian groups and hyperbolic geometry published in the Bulletin of the American Mathematical...

is an isomorphism of differentiable manifolds. It is an invertible function that maps one differentiable manifold to another such that both the function...

intersection with S; if there exists such a subset, then (M, g) is called globally hyperbolic. The following is automatically true of a Cauchy surface S: The subset...

Since Teichmüller space is a complex manifold it carries a Carathéodory metric. Teichmüller space is Kobayashi hyperbolic and its Kobayashi metric coincides...

studying systolic invariants of manifolds and polyhedra. Systolic hyperbolic geometry the study of systoles in hyperbolic geometry. Contents:  Top A B C...