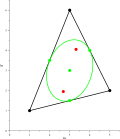
In mathematics, Marden's theorem, named after Morris Marden but proved about 100 years earlier by Jörg Siebeck, gives a geometric relationship between...

_{j=1}^{n}|z-a_{j}|^{-2}}}a_{i}} Marden's theorem Bôcher's theorem Sendov's conjecture Routh–Hurwitz theorem Hurwitz's theorem (complex analysis) Descartes'...

triangle's Steiner inellipse can be found as follows, according to Marden's theorem: Denote the triangle's vertices in the complex plane as a = xA + yAi...

West Sussex Marden Park, Surrey Marden (surname) Marden's theorem, in complex geometry River Marden, Wiltshire, England Marsden (disambiguation) Madsen...

theorem (complex analysis) Marden's theorem Nyquist stability criterion Pole–zero plot Residue (complex analysis) Rouché's theorem Sendov's conjecture Conway...

interior to the triangle and tangent at the midpoints of the sides. Marden's theorem shows how to find the foci of this ellipse. This ellipse has the greatest...

{a^{4}+b^{4}+c^{4}-a^{2}b^{2}-b^{2}c^{2}-c^{2}a^{2}}}.} According to Marden's theorem, if the three vertices of the triangle are the complex zeros of a cubic...

Hölder discovered it independently, and published it in 1889. Marden's theorem. This theorem relating the location of the zeros of a complex cubic polynomial...

scaled fundamental solution for the Laplacian in that domain. Marden's theorem Marden, Morris (1951-05-01). "Book Review: The location of critical points...

function f ( x ) = ‖ x ‖ 2 − 1 {\displaystyle f(x)=\Vert x\Vert ^{2}-1} . Marden's theorem Root-finding algorithm Sendov's conjecture Vanish at infinity Zero...

Function under the supervision of Joseph L. Walsh. He is known for the Marden's theorem, which was proven by Jörg Siebeck.[failed verification] His publications...

complex conjugates, appear symmetrically above and below the real axis.) Marden's theorem says that the points representing the roots of the derivative of the...

rule of signs – Counting polynomial real roots based on coefficients Marden's theorem – On zeros of derivatives of cubic polynomials Newton's identities –...

theorem (complex analysis) Manin–Drinfeld theorem (number theory) Mann's theorem (number theory) Marcinkiewicz theorem (functional analysis) Marden's...

JSTOR 1971059, MR 0349992, Zbl 0282.30014 Canary, Richard D. (2010). "Marden's Tameness Conjecture: history and applications". arXiv:1008.0118 [math.GT]...

and hence unique. The theorem was proven for closed manifolds by Mostow (1968) and extended to finite volume manifolds by Marden (1974) in 3 dimensions...

homeomorphic to the interior of a compact 3-manifold. The tameness theorem was conjectured by Marden (1974). It was proved by Agol (2004) and, independently, by...

S2CID 126002045. Kalman, Dan (April 2008). "An Elementary Proof of Marden's Theorem" (PDF). American Mathematical Monthly. 115 (4): 330–338. doi:10.1080/00029890...

In mathematics, Cohn's theorem states that a nth-degree self-inversive polynomial p ( z ) {\displaystyle p(z)} has as many roots in the open unit disk...

homeomorphic to the interior of a compact 3-manifold. The tameness theorem was conjectured by Marden. It was proved by Agol and, independently, by Danny Calegari...

Epstein & Marden (1987). Weeks (1993). Rousseeuw, Ruts & Tukey (1999). Harris (1971). Pulleyblank (1983); see especially remarks following Theorem 2.9. Katoh...

In complex analysis, de Branges's theorem, or the Bieberbach conjecture, is a theorem that gives a necessary condition on a holomorphic function in order...

Kleinian group is geometrically tame, so the Ahlfors conjecture follows from Marden's tameness conjecture that hyperbolic 3-manifolds with finitely generated...

Ahlfors measure conjecture Density theorem for Kleinian groups Ending lamination theorem Tameness theorem (Marden's conjecture) Bers, Lipman (1970), "On...

contributions to abstract algebra. She proved Noether's first and second theorems, which are fundamental in mathematical physics. She was described by Pavel...

In hyperbolic geometry, the ending lamination theorem, originally conjectured by William Thurston (1982), states that hyperbolic 3-manifolds with finitely...

results related to Mostow's theorem on rigidity Chapter 6 describes Gromov's invariant and his proof of Mostow's theorem. Chapter 7 (by Milnor) describes...

first proof of this conjecture, now known as the Denjoy–Carleman–Ahlfors theorem. It states that the number of asymptotic values approached by an entire...

1090/S0002-9939-1952-0047828-8. ISSN 0002-9939. Pless 1990, pg. 75, Theorem 48 Pless 1990, pg. 77, Theorem 51 Pless, Vera (1990), Introduction to the Theory of Error...

distance no more than 1 from at least one critical point. The Gauss–Lucas theorem says that all of the critical points lie within the convex hull of the...