An orthogonal wavelet is a wavelet whose associated wavelet transform is orthogonal. That is, the inverse wavelet transform is the adjoint of the wavelet...

The Daubechies wavelets, based on the work of Ingrid Daubechies, are a family of orthogonal wavelets defining a discrete wavelet transform and characterized...

wavelet Legendre wavelet Villasenor wavelet Symlet Beta wavelet Hermitian wavelet Meyer wavelet Mexican hat wavelet Poisson wavelet Shannon wavelet Spline...

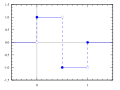
mathematics, the Haar wavelet is a sequence of rescaled "square-shaped" functions which together form a wavelet family or basis. Wavelet analysis is similar...

continuous wavelets are used for both wavelet decomposition and composition transforms. That is they are the continuous counterpart of orthogonal wavelets. The...

research, a wavelet transform is introduced to replace the DFT as the method of creating orthogonal frequencies. This is due to the advantages wavelets offer...

domain into a sequence of coefficients based on an orthogonal basis of small finite waves, or wavelets. The transform can be easily extended to multidimensional...

spline wavelets introduced by C.K. Chui and J.Z. Wang are based on a certain spline interpolation formula. Though these wavelets are orthogonal, they do...

(nearly orthogonal) Chirplet transform Complex wavelet transform Constant-Q transform Continuous wavelet transform Daubechies wavelet Discrete wavelet transform...

discrete wavelets designed by Ingrid Daubechies, at the request of Ronald Coifman, to have scaling functions with vanishing moments. The wavelet is near...

analysis, a discrete wavelet transform (DWT) is any wavelet transform for which the wavelets are discretely sampled. As with other wavelet transforms, a key...

Biorthogonal wavelet is a wavelet where the associated wavelet transform is invertible but not necessarily orthogonal. Designing biorthogonal wavelets allows...

Cohen–Daubechies–Feauveau wavelets are a family of biorthogonal wavelets that was made popular by Ingrid Daubechies. These are not the same as the orthogonal Daubechies...

properly an orthonormal binomial quadrature mirror filter – is an orthogonal wavelet developed in 1990. The binomial QMF bank with perfect reconstruction...

(SB-TS), also called wavelet packet decomposition (WPD; sometimes known as just wavelet packets or subband tree), is a wavelet transform where the discrete-time...

applied for Gabor wavelets, since this requires computation of bi-orthogonal wavelets, which may be very time-consuming. Therefore, usually, a filter bank...

{e^{i2\pi t}-1}{i2\pi t}}.} The function φ is orthogonal to itself for different k and is also orthogonal to the wavelet functions for non-negative j: ∫ − ∞ ∞...

known to be an orthonormal wavelet, Strömberg wavelet was the first smooth orthonormal wavelet to be discovered. The term wavelet had not been coined at the...

The Meyer wavelet is an orthogonal wavelet proposed by Yves Meyer. As a type of a continuous wavelet, it has been applied in a number of cases, such as...

uncertainty in information carried by this wavelet is minimized. However they have the downside of being non-orthogonal, so efficient decomposition into the...

the unit disk and have orthogonality of both radial and angular parts. Walsh functions and Haar wavelets are examples of orthogonal functions with discrete...

complex wavelets in image processing was originally set up in 1995 by J.M. Lina and L. Gagnon in the framework of the Daubechies orthogonal filters banks...

In mathematics, a dual wavelet is the dual to a wavelet. In general, the wavelet series generated by a square-integrable function will have a dual series...

inner-product space Orthogonal polynomials Fourier analysis and Fourier series Harmonic analysis Orthogonal wavelet Biorthogonal wavelet Radial basis function...

high-pass and low-pass filters is equal to 1. Orthogonal wavelets – the Haar wavelets and related Daubechies wavelets, Coiflets, and some developed by Mallat...

the Shannon wavelet (or sinc wavelets) is a decomposition that is defined by signal analysis by ideal bandpass filters. Shannon wavelet may be either...

polynomials are a classical orthogonal polynomial sequence. The polynomials arise in: signal processing as Hermitian wavelets for wavelet transform analysis probability...

replace the DFT as the method of creating non-orthogonal frequencies. This is due to the advantages wavelets offer, which are particularly useful on noisy...

expansions of powers of binomials Binomial QMF, a perfect-reconstruction orthogonal wavelet decomposition Binomial theorem, a theorem about powers of binomials...

is defined as the (closed) linear hull of the mother wavelet's integer shifts, is the orthogonal complement to V 0 {\displaystyle V_{0}} inside V − 1...