In mathematics, the qualifier pointwise is used to indicate that a certain property is defined by considering each value f ( x ) {\displaystyle f(x)}...

In mathematics, pointwise convergence is one of various senses in which a sequence of functions can converge to a particular function. It is weaker than...

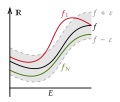
uniform convergence is a mode of convergence of functions stronger than pointwise convergence. A sequence of functions ( f n ) {\displaystyle (f_{n})} converges...

In statistics, probability theory and information theory, pointwise mutual information (PMI), or point mutual information, is a measure of association...

is almost everywhere pointwise convergent to a function then the sequence converges in L 1 {\displaystyle L_{1}} to its pointwise limit, and in particular...

operators (and thus bounded operators) whose domain is a Banach space, pointwise boundedness is equivalent to uniform boundedness in operator norm. The...

equicontinuous and converges pointwise to a function (not necessarily continuous a-priori). In particular, the limit of an equicontinuous pointwise convergent sequence...

set X into a vector space has a natural vector space structure given by pointwise addition and scalar multiplication. In other scenarios, the function space...

In mathematics, the lower envelope or pointwise minimum of a finite set of functions is the pointwise minimum of the functions, the function whose value...

provides an analogous example showing that polyhedral surfaces that converge pointwise to a curved surface do not necessarily converge to its area, even when...

turned into a vector space under the operations of pointwise addition of functions and pointwise scalar multiplication. All sequence spaces are linear...

convergence in distribution of the sequence of random variables with pointwise convergence of their characteristic functions. This theorem is the basis...

a group of loops in a topological group G with multiplication defined pointwise. In its most general form a loop group is a group of continuous mappings...

to occur. Determination of convergence requires the comprehension of pointwise convergence, uniform convergence, absolute convergence, Lp spaces, summability...

is a result that says, heuristically, whenever certain curvatures are pointwise constant then they are forced to be globally constant. The proof is essentially...

Riemann curvature tensor. A manifold M n {\displaystyle M^{n}} is called pointwise Osserman if, for every p ∈ M n {\displaystyle p\in M^{n}} , the spectrum...

producing bounds on the CDF, we must differentiate between pointwise and simultaneous bands. A pointwise CDF bound is one which only guarantees their Coverage...

-topology on F {\displaystyle F} is called the topology of pointwise convergence. The topology of pointwise convergence on F {\displaystyle F} is identical to...

fundamental result in mathematical analysis establishing the (Lebesgue) pointwise almost everywhere convergence of Fourier series of L2 functions, proved...

called pointwise limit, denoted x n , m → y m pointwise {\displaystyle x_{n,m}\to y_{m}\quad {\text{pointwise}}} , or lim n → ∞ x n , m = y m pointwise {\displaystyle...

In natural language processing and information retrieval, cluster labeling is the problem of picking descriptive, human-readable labels for the clusters...

Egorov's theorem establishes a condition for the uniform convergence of a pointwise convergent sequence of measurable functions. It is also named Severini–Egoroff...

{\tfrac {n}{P}}x}\,dx.} The series does not necessarily converge (in the pointwise sense) and, even if it does, it is not necessarily equal to s ( x ) {\displaystyle...

his research contributions include pointwise convergence of averages along cubes, being “the first complete pointwise convergence result obtained in the...

Then: the sequence { g n ( x ) } n {\displaystyle \{g_{n}(x)\}_{n}} is pointwise non-decreasing at any x and g n ≤ f n {\displaystyle g_{n}\leq f_{n}}...

relativity, a frame field (also called a tetrad or vierbein) is a set of four pointwise-orthonormal vector fields, one timelike and three spacelike, defined on...

Rank approaches are often categorized using one of three approaches: pointwise (where individual documents are ranked), pairwise (where pairs of documents...

) = g ( y ) pointwise . {\displaystyle \lim _{x\to p}f(x,y)=g(y)\;\;{\text{pointwise}}.} Alternatively, we may say f tends to g pointwise as x approaches...

mathematicians consider real and imaginary parts of complex sequences, or by pointwise evaluation of operator sequences.[clarification needed] Many of the theorems...

on the circle, Hεf converges uniformly to Hf, so in particular pointwise. The pointwise limit is a Cauchy principal value, written H f = P . V . 1 π ∫...