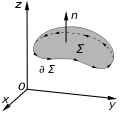
Stokes' theorem, also known as the Kelvin–Stokes theorem after Lord Kelvin and George Stokes, the fundamental theorem for curls or simply the curl theorem...

the generalized Stokes theorem (sometimes with apostrophe as Stokes' theorem or Stokes's theorem), also called the Stokes–Cartan theorem, is a statement...

special case of Stokes' theorem (surface in R 3 {\displaystyle \mathbb {R} ^{3}} ). In one dimension, it is equivalent to the fundamental theorem of calculus...

integral theorem and Cauchy's integral formula. The residue theorem should not be confused with special cases of the generalized Stokes' theorem; however...

relativity). Kelvin–Stokes theorem Generalized Stokes theorem Differential form Katz, Victor J. (1979). "The history of Stokes's theorem". Mathematics Magazine...

Stokes law can refer to: Stokes' law, for friction force Stokes' law (sound attenuation), describing attenuation of sound in Newtonian liquids Stokes'...

Stokes, 1st Baronet, FRS (/stoʊks/; 13 August 1819 – 1 February 1903) was an Irish mathematician and physicist. Born in County Sligo, Ireland, Stokes...

a natural, metric-independent generalization of Stokes' theorem, Gauss's theorem, and Green's theorem from vector calculus. If a differential k-form is...

Stokes shift Stokes stream function Stokes' theorem Stokes wave Campbell–Stokes recorder Navier–Stokes equations Stokes Bay (disambiguation) Stokes Township...

Brouwer's fixed-point theorem is a fixed-point theorem in topology, named after L. E. J. (Bertus) Brouwer. It states that for any continuous function f...

\,\mathbf {q} ]}\nabla \varphi (\mathbf {r} )\cdot d\mathbf {r} .} Stokes' theorem relates the surface integral of the curl of a vector field F over a...

Stokes. They were developed over several decades of progressively building the theories, from 1822 (Navier) to 1842–1850 (Stokes). The Navier–Stokes equations...

theorem of calculus, the divergence theorem, Green's theorem, and Stokes' theorem as special cases of a single general result, the generalized Stokes...

vector fields. The corresponding form of the fundamental theorem of calculus is Stokes' theorem, which relates the surface integral of the curl of a vector...

Poincaré–Hopf theorem (also known as the Poincaré–Hopf index formula, Poincaré–Hopf index theorem, or Hopf index theorem) is an important theorem that is used...

C {\displaystyle C} , allows us to state the celebrated Stokes' theorem (Stokes–Cartan theorem) for chains in a subset of R m {\displaystyle \mathbb {R}...

Lord Kelvin to Sir George Stokes containing the first disclosure of the classical Stokes' theorem (i.e., the Kelvin–Stokes theorem). Calculus on Manifolds...

horn Jacobian matrix Hessian matrix Curvature Green's theorem Divergence theorem Stokes' theorem Vector Calculus Infinite series Maclaurin series, Taylor...

The fundamental theorem of calculus is a theorem that links the concept of differentiating a function (calculating its slopes, or rate of change at each...

and Stokes' theorem simultaneously generalizes the three theorems of vector calculus: the divergence theorem, Green's theorem, and the Kelvin-Stokes theorem...

The proof of Cauchy's integral theorem for higher dimensional spaces relies on the using the generalized Stokes theorem on the quantity G(r, r′) f(r′)...

calculus, and more generally differential geometry, Stokes' theorem (also called the generalized Stokes' theorem) is a statement about the integration of differential...

{\displaystyle {\boldsymbol {\omega }}=\nabla \times \mathbf {V} .} By Stokes' theorem, the flux of curl or vorticity vectors through a surface S is equal...

and vector calculus, such as the divergence theorem, magnetic flux, and its generalization, Stokes' theorem. Let us notice that we defined the surface...

first term, we substitute from the governing equation, and then apply Stokes' theorem, thus: ∮ C D u D t ⋅ d s = ∫ A ∇ × ( − 1 ρ ∇ p + ∇ Φ ) ⋅ n d S = ∫...

2-forms, respectively, and the key theorems of vector calculus are all special cases of the general form of Stokes' theorem. From the point of view of both...

form". The forms are exactly equivalent, and related by the Kelvin–Stokes theorem (see the "proof" section below). Forms using SI units, and those using...

embodied by the integral theorems of vector calculus:: 543ff  Gradient theorem Stokes' theorem Divergence theorem Green's theorem. In a more advanced study...

\iint _{S}\left(\nabla \times \mathbf {A} \right)\cdot d\mathbf {S} } (Stokes' theorem) ∮ ∂ S ψ d ℓ   =   − ∬ S ∇ ψ × d S {\displaystyle \oint _{\partial...

The gradient theorem, also known as the fundamental theorem of calculus for line integrals, says that a line integral through a gradient field can be evaluated...