Circle packing in a circle is a two-dimensional packing problem with the objective of packing unit circles into the smallest possible larger circle. If...

In geometry, circle packing is the study of the arrangement of circles (of equal or varying sizes) on a given surface such that no overlapping occurs...

Circle packing in a square is a packing problem in recreational mathematics where the aim is to pack n unit circles into the smallest possible square...

The circle packing theorem (also known as the Koebe–Andreev–Thurston theorem) describes the possible tangency relations between circles in the plane whose...

squares can be packed into some larger shape, often a square or circle. Square packing in a square is the problem of determining the maximum number of unit...

three-dimensional equivalent of the circle packing in a circle problem in two dimensions. Best packing of m>1 equal spheres in a sphere setting a new density record...

In mathematics, a Ford circle is a circle in the Euclidean plane, in a family of circles that are all tangent to the x {\displaystyle x} -axis at rational...

Circle packing – Field of geometry closely arranging circles on a plane Circle packing in a circle – Two-dimensional packing problem Circle packing in...

An osculating circle is a circle that best approximates the curvature of a curve at a specific point. It is tangent to the curve at that point and has...

mathematics Circle packing in an equilateral triangle is a packing problem in discrete mathematics where the objective is to pack n unit circles into the...

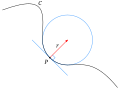
The circles of Apollonius are any of several sets of circles associated with Apollonius of Perga, a renowned Greek geometer. Most of these circles are...

the ideas in the circle packing theorem. The related circle packing problem deals with packing circles, possibly of different sizes, on a surface, for...

In mathematics, an Apollonian gasket, Apollonian net, or Apollonian circle packing is a fractal generated by starting with a triple of circles, each tangent...

2 {\displaystyle C=2} in spherical geometry and C = − 2 {\displaystyle C=-2} in hyperbolic geometry. Circle packing in a circle Euler's four-square identity...

sphere packing problems can be generalised to consider unequal spheres, spaces of other dimensions (where the problem becomes circle packing in two dimensions...

have been packing stones used to support the larger stones when the circle was constructed and would originally have been buried. Differences in opinion...

to Circle Packing: The Theory of Discrete Analytic Functions is a mathematical monograph concerning systems of tangent circles and the circle packing theorem...

In geometry, the Malfatti circles are three circles inside a given triangle such that each circle is tangent to the other two and to two sides of the...

is a generalization of Apollonius' problem, whereas Soddy's hexlet is a generalization of a Steiner chain. Tangent lines to circles Circle packing theorem...

In geometry, an Archimedean circle is any circle constructed from an arbelos that has the same radius as each of Archimedes' twin circles. If the arbelos...

An overlapping circles grid is a geometric pattern of repeating, overlapping circles of an equal radius in two-dimensional space. Commonly, designs are...

seen as a source of that ice and meat packing moved across the line, creating processing plants and ice house. Gary is on both routes of the Circle Tour...

Melbourne's northern outskirts, and a fresh fruit packing operation in Griffith, New South Wales. Golden Circle manufactures more than 800 products including...

In geometry, the Soddy circles of a triangle are two circles associated with any triangle in the plane. Their centers are the Soddy centers of the triangle...

In Euclidean plane geometry, Apollonius's problem is to construct circles that are tangent to three given circles in a plane (Figure 1). Apollonius of...

equivalent of the circle packing in a square problem in two dimensions. The problem consists of determining the optimal packing of a given number of spheres...

corresponding circles in this circle packing. Every convex polyhedron has a combinatorially equivalent polyhedron, the canonical polyhedron, that does have a midsphere...

In geometry, Coxeter's loxodromic sequence of tangent circles is an infinite sequence of circles arranged so that any four consecutive circles in the...

double lattice packing shown. In a preprint released in 2016, Thomas Hales and Wöden Kusner announced a proof that this double lattice packing of the regular...

Circle packing in a right isosceles triangle is a packing problem where the objective is to pack n unit circles into the smallest possible isosceles right...