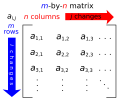
graph theory, the Laplacian matrix, also called the graph Laplacian, admittance matrix, Kirchhoff matrix or discrete Laplacian, is a matrix representation...

of a submatrix of the graph's Laplacian matrix; specifically, the number is equal to any cofactor of the Laplacian matrix. Kirchhoff's theorem is a generalization...

adjacency matrix to construct the Laplacian matrix of a graph: the Laplacian matrix is the difference of the degree matrix and the adjacency matrix. Given...

relevant eigenvectors of a Laplacian matrix of A {\displaystyle A} . There are many different ways to define a Laplacian which have different mathematical...

vertices), the discrete Laplace operator is more commonly called the Laplacian matrix. The discrete Laplace operator occurs in physics problems such as the...

In mathematics, the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a scalar function on Euclidean...

Hermitian Laplacian matrix is a key tool in this context, as it is used to analyze the spectra of mixed graphs. The Hermitian-adjacency matrix of a mixed...

such as its adjacency matrix or Laplacian matrix. The adjacency matrix of a simple undirected graph is a real symmetric matrix and is therefore orthogonally...

matrix, while requiring time proportional to the minimum degree of the two vertices with the adjacency list. Laplacian matrix Self-similarity matrix Biggs...

Fourier transform is a mathematical transform which eigendecomposes the Laplacian matrix of a graph into eigenvalues and eigenvectors. Analogously to the classical...

{\displaystyle A/B=((A/C)/(B/C))} . The Schur complement of a Laplacian matrix is also a Laplacian matrix. The Schur complement arises naturally in solving a system...

second-smallest eigenvalue (counting multiple eigenvalues separately) of the Laplacian matrix of G. This eigenvalue is greater than 0 if and only if G is a connected...

therefore the rows of the matrix sum to zero. Up to a global sign, a large class of examples of such matrices is provided by the Laplacian of a directed, weighted...

The Hessian matrix is commonly used for expressing image processing operators in image processing and computer vision (see the Laplacian of Gaussian (LoG)...

vector calculus, the Jacobian matrix (/dʒəˈkoʊbiən/, /dʒɪ-, jɪ-/) of a vector-valued function of several variables is the matrix of all its first-order partial...

the Moore–Penrose inverse, L the Laplacian matrix of G, |V| is the number of vertices in G, and Φ is the |V| × |V| matrix containing all 1s. If i = j then...

of the adjacency matrix, or spectral clustering that groups graph vertices using the eigendecomposition of the graph Laplacian matrix. A multi-level graph...

related to the eigenvalues of the network's Laplacian matrix. Let A {\displaystyle {\bf {A}}} be the adjacency matrix describing the topological structure of...

admittance matrix is used in the formulation of the power flow problem. The nodal admittance matrix of a power system is a form of Laplacian matrix of the...

eigenvalue of the graph's adjacency matrix A {\displaystyle A} , or (increasingly) of the graph's Laplacian matrix due to its discrete Laplace operator...

in the context of graph theory). Laplacian matrix — a matrix equal to the degree matrix minus the adjacency matrix for a graph, used to find the number...

diagonal matrix with D i i = ∑ j = 1 ℓ + u W i j {\displaystyle D_{ii}=\sum _{j=1}^{\ell +u}W_{ij}} and L {\displaystyle L} to be the Laplacian matrix D −...

In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero; the term usually refers to square matrices...

in such settings (e.g., Laplacian Eigenmaps, LLE) as special cases of kernel PCA by constructing a data-dependent kernel matrix. KPCA has an internal model...

determinant of a matrix derived from the graph, using Kirchhoff's matrix-tree theorem. Specifically, to compute t(G), one constructs the Laplacian matrix of the...

by a cofactor of the Laplacian matrix. However, the Laplacian characteristic polynomial does not satisfy DC. By studying Laplacians with vertex weights...

adjacency matrix of a complete bipartite graph Km,n has eigenvalues √nm, −√nm and 0; with multiplicity 1, 1 and n + m − 2 respectively. The Laplacian matrix of...

largest (or smallest) eigenvalues and corresponding eigenvectors of the Laplacian matrix of the graph and then use those for actually placing the nodes. Usually...

In mathematics, matrix calculus is a specialized notation for doing multivariable calculus, especially over spaces of matrices. It collects the various...

the nullity of the Laplacian matrix of the graph, defined as L = D − A, where D is the diagonal matrix of vertex degrees; the Laplacian nullity equals the...