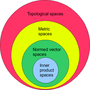
mathematics, a normed vector space or normed space is a vector space over the real or complex numbers on which a norm is defined. A norm is a generalization...

In mathematics, a norm is a function from a real or complex vector space to the non-negative real numbers that behaves in certain ways like the distance...

of mathematics, norms are defined for elements within a vector space. Specifically, when the vector space comprises matrices, such norms are referred to...

In mathematics, a unit vector in a normed vector space is a vector (often a spatial vector) of length 1. A unit vector is often denoted by a lowercase...

normed vector space. Thus, a Banach space is a vector space with a metric that allows the computation of vector length and distance between vectors and...

space of bounded linear operators between two given normed vector spaces. Informally, the operator norm ‖ T ‖ {\displaystyle \|T\|} of a linear map T : X...

function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces. They are sometimes called Lebesgue spaces, named after...

|y|} in the picture); so, every inner product space is a normed vector space. If this normed space is also complete (that is, a Banach space) then the...

topological vector spaces, which include function spaces, inner product spaces, normed spaces, Hilbert spaces and Banach spaces. In this article, vectors are...

the dual norm is a measure of size for a continuous linear function defined on a normed vector space. Let X {\displaystyle X} be a normed vector space with...

{\displaystyle B_{1}[p]=X} for any p ∈ X . {\displaystyle p\in X.} Any normed vector space V with norm ‖ ⋅ ‖ {\displaystyle \|\cdot \|} is also a metric space with...

space is a normed vector space, and the inner product of a vector with itself is real and positive-definite. The dot product is defined for vectors that have...

applied as the measure of units between a number and zero. In vector spaces, the Euclidean norm is a measure of magnitude used to define a distance between...

v by k. A vector space equipped with a norm is called a normed vector space (or normed linear space). The norm is usually defined to be an element of...

other geometries, the triangle inequality is a theorem about vectors and vector lengths (norms): ‖ u + v ‖ ≤ ‖ u ‖ + ‖ v ‖ , {\displaystyle \|\mathbf {u}...

structure of gradation Normed vector space, a vector space on which a norm is defined Hilbert space Ordered vector space, a vector space equipped with a...

topological vector spaces. They are generalizations of Banach spaces (normed vector spaces that are complete with respect to the metric induced by the norm). All...

{\displaystyle Y.} If X {\displaystyle X} and Y {\displaystyle Y} are normed vector spaces (a special type of TVS), then L {\displaystyle L} is bounded...

convex topological vector spaces (LCTVS) or locally convex spaces are examples of topological vector spaces (TVS) that generalize normed spaces. They can...

a length or size to any vector in a vector space Matrix norm, a map that assigns a length or size to a matrix Operator norm, a map that assigns a length...

and its vector part: q = q s + q → v . {\displaystyle q=q_{s}+{\vec {q}}_{v}.} Decompose the vector part further as the product of its norm and its versor:...

Every normed vector space has a natural topological structure: the norm induces a metric and the metric induces a topology. This is a topological vector space...

Vector notation In mathematics and physics, vector notation is a commonly used notation for representing vectors, which may be Euclidean vectors, or more...

complex normed vector spaces do not have inner products, but all normed vector spaces have norms (by definition). For example, a commonly used norm for a...

restriction of a seminorm (respectively, norm) to a vector subspace is once again a seminorm (respectively, norm). If p : X → R {\displaystyle p:X\to \mathbb...

admit the structure of a metric space, including Riemannian manifolds, normed vector spaces, and graphs. In abstract algebra, the p-adic numbers arise as...

In mathematics, any vector space V {\displaystyle V} has a corresponding dual vector space (or just dual space for short) consisting of all linear forms...

is formed by the study of vector spaces endowed with some kind of limit-related structure (for example, inner product, norm, or topology) and the linear...

physics, and engineering, a Euclidean vector or simply a vector (sometimes called a geometric vector or spatial vector) is a geometric object that has magnitude...

bound on the inner product between two vectors in an inner product space in terms of the product of the vector norms. It is considered one of the most important...