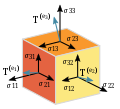
If a tensor A is defined on a vector fields set X(M) over a module M, we call A a tensor field on M. Many mathematical structures called "tensors" are...

electromagnetism, the electromagnetic tensor or electromagnetic field tensor (sometimes called the field strength tensor, Faraday tensor or Maxwell bivector) is a...

(electromagnetic tensor, Maxwell tensor, permittivity, magnetic susceptibility, ...), and general relativity (stress–energy tensor, curvature tensor, ...). In...

the tensor product of two fields is their tensor product as algebras over a common subfield. If no subfield is explicitly specified, the two fields must...

numbers), and a metric field on M consists of a metric tensor at each point p of M that varies smoothly with p. A metric tensor g is positive-definite...

In science, a field is a physical quantity, represented by a scalar, vector, or tensor, that has a value for each point in space and time. An example of...

stress-energy tensor The stress–energy tensor, sometimes called the stress–energy–momentum tensor or the energy–momentum tensor, is a tensor physical quantity...

In the mathematical field of differential geometry, the Riemann curvature tensor or Riemann–Christoffel tensor (after Bernhard Riemann and Elwin Bruno...

two vectors is sometimes called an elementary tensor or a decomposable tensor. The elementary tensors span V ⊗ W {\displaystyle V\otimes W} in the sense...

mathematics, the modern component-free approach to the theory of a tensor views a tensor as an abstract object, expressing some definite type of multilinear...

Tensor fields, which associate a tensor to every point in space. For example, in general relativity gravitation is associated with the tensor field called...

Riemann curvature tensor, the Weyl tensor expresses the tidal force that a body feels when moving along a geodesic. The Weyl tensor differs from the Riemann...

is a vector field. If T {\displaystyle {\boldsymbol {T}}} is a tensor field of order n > 1 then the divergence of the field is a tensor of order n− 1...

differential geometry, the Einstein tensor (named after Albert Einstein; also known as the trace-reversed Ricci tensor) is used to express the curvature...

covariant derivative of a tensor field along a vector field v is again a tensor field of the same type. Explicitly, let T be a tensor field of type (p, q). Consider...

In multilinear algebra, a tensor contraction is an operation on a tensor that arises from the canonical pairing of a vector space and its dual. In components...

Einstein in 1915 in the form of a tensor equation which related the local spacetime curvature (expressed by the Einstein tensor) with the local energy, momentum...

element for the tensor space. The tensor is the sum of its components multiplied by their corresponding basis elements. Tensors and tensor fields can be expressed...

completely antisymmetric contravariant tensor field may be referred to as a k {\displaystyle k} -vector field. A tensor A that is antisymmetric on indices...

geometry, a tensor density or relative tensor is a generalization of the tensor field concept. A tensor density transforms as a tensor field when passing...

universal property of the tensor product of vector spaces extends to more general situations in abstract algebra. The tensor product of an algebra and...

of tensor theory. For expositions of tensor theory from different points of view, see: Tensor Tensor (intrinsic definition) Application of tensor theory...

a Killing tensor or Killing tensor field is a generalization of a Killing vector, for symmetric tensor fields instead of just vector fields. It is a concept...

Let V be a vector space over a field K. For any nonnegative integer k, we define the kth tensor power of V to be the tensor product of V with itself k times:...

In theoretical particle physics, the gluon field strength tensor is a second order tensor field characterizing the gluon interaction between quarks. The...

the Einstein tensor, G a b = R a b − 1 2 R g a b {\displaystyle G_{ab}\,=R_{ab}-{\frac {1}{2}}Rg_{ab}} written in terms of the Ricci tensor Rab and Ricci...

manifold M {\displaystyle M} and the metric tensor is given as a covariant, second-degree, symmetric tensor on M {\displaystyle M} , conventionally denoted...

the change of a tensor field (including scalar functions, vector fields and one-forms), along the flow defined by another vector field. This change is...

the nonmetricity tensor in differential geometry is the covariant derivative of the metric tensor. It is therefore a tensor field of order three. It...

relationship between the Ricci tensor and the matter content of the universe. Like the metric tensor, the Ricci tensor assigns to each tangent space of...