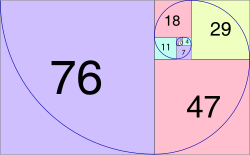
In mathematics, the Wythoff array is an infinite matrix of positive integers derived from the Fibonacci sequence and named after Dutch mathematician Willem...

Subtract a square Wythoff array Wythoff's game at Cut-the-knot, quoting Martin Gardner's book Penrose Tiles to Trapdoor Ciphers Wythoff, W. A. (1907), "A...

Wythoff array, a two-dimensional array of numbers related to this game and to the Fibonacci sequence, is also named after him. In geometry, Wythoff is...

Randomized mathematical sequence based upon the Fibonacci sequence Wythoff array – Infinite matrix of integers derived from the Fibonacci sequence International...

a shift by a finite number of positions) as one of the rows of the Wythoff array. The Fibonacci sequence itself is the first row, and a shift of the...

Fibonacci-like integer sequences appear in shifted form as a row of the Wythoff array; the Fibonacci sequence itself is the first row and the Lucas sequence...

sequences define the optimal strategy for Wythoff's game, and are used in the definition of the Wythoff array. As another example, for the square root...

sequence A003603 (Fractal sequence obtained from Fibonacci numbers (or Wythoff array)) OEIS sequence A112382 (Self-descriptive fractal sequence: the sequence...

wabweb.net (in German). Retrieved 2024-11-09. Gernsback, Hugo (2016), Wythoff, Grant (ed.), "Results of the $500.00 Prize Contest: Who Will Save the...

the row's element. The diagonal f-vector numbers are derived through the Wythoff construction, dividing the full group order of a subgroup order by removing...

honeycombs in three dimensions. Uniform honeycombs can be constructed using the Wythoff construction. The Schmitt-Conway biprism is a convex polyhedron with the...

the row's element. The diagonal f-vector numbers are derived through the Wythoff construction, dividing the full group order of a subgroup order by removing...

elements are shown. The diagonal f-vector numbers are derived through the Wythoff construction, dividing the full group order of a subgroup order by removing...

1 , ± 1 φ 3 , ± 1 ) ( ± 1 φ , ± 1 φ 2 , ± 2 φ ) {\displaystyle {\begin{array}{ccclc}{\Bigl (}&\pm \,{\frac {1}{\varphi ^{2}}},&0,&\pm {\bigl [}2-{\frac...

± φ , ± 1 φ , ± 2 φ ) ( ± 1 φ 2 , ± 1 φ , ± 2 ) {\displaystyle {\begin{array}{crclc}{\Bigl (}&0,&\pm \,\varphi ,&\pm {\bigl [}2-{\frac {1}{\varphi }}{\bigr...

constructed in one or more reflective point group in 4 dimensions by a Wythoff construction, represented by rings around permutations of nodes in a Coxeter...

the row's element. The diagonal f-vector numbers are derived through the Wythoff construction, dividing the full group order of a subgroup order by removing...

φ , ± 1 φ 3 ) ( ± [ 1 + 1 φ 2 ] , ± 1 , ± 2 φ ) {\displaystyle {\begin{array}{crccc}{\Bigl (}&\pm \,1,&0,&\pm \,{\frac {3}{\varphi }}&{\Bigr )}\\{\Bigl...

Essays, Dover Publications, 1999, ISBN 978-0-486-40919-1 (Chapter 3: Wythoff's Construction for Uniform Polytopes) Norman Johnson Uniform Polytopes,...

2 , ± φ 2 ) , ( ± φ 2 , ± 1 , ± [ 3 φ − 2 ] ) , {\displaystyle {\begin{array}{crrlc}{\Bigl (}&\pm {\bigl [}2-{\frac {1}{\varphi }}{\bigr ]},&\pm \,1...

Spherical polygons play an important role in cartography (map making) and in Wythoff's construction of the uniform polyhedra. A skew polygon does not lie in...

elements are shown. The diagonal f-vector numbers are derived through the Wythoff construction, dividing the full group order of a subgroup order by removing...

the row's element. The diagonal f-vector numbers are derived through the Wythoff construction, dividing the full group order of a subgroup order by removing...

\end{array}}} and an even number of minus signs in these two sets: ( ± 2 φ , ± φ , ± [ 1 + 2 φ ] ) , ( ± φ , ± 3 , ± 2 φ ) , {\displaystyle {\begin{array}{ccccccc}{\Bigl...

elements are shown. The diagonal f-vector numbers are derived through the Wythoff construction, dividing the full group order of a subgroup order by removing...

± 5 , ± 2 , ± 5 φ ) , ( ± 1 φ , ± 3 , ± 2 φ ) , {\displaystyle {\begin{array}{ccclc}{\Bigl (}&\pm \,\varphi ,&\pm \,\varphi ,&\pm {\bigl [}3-{\frac {1}{\varphi...

shell neighbors or the central sphere is √2. There are five different Wythoff constructions of this tessellation as a uniform polytope. They are geometrically...

, φ 2 ) , ( φ 2 , 1 φ 2 , 2 ) , ( 5 , 1 , 5 ) . {\displaystyle {\begin{array}{lcr}{\Bigl (}1,&1,&3{\Bigr )},\\{\Bigl (}{\frac {1}{\varphi }},&{\frac...