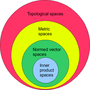
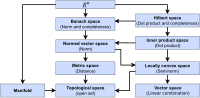
In mathematics, a metric space is a set together with a notion of distance between its elements, usually called points. The distance is measured by a function...

a metric space M is called complete (or a Cauchy space) if every Cauchy sequence of points in M has a limit that is also in M. Intuitively, a space is...

them. Formally, a Riemannian metric (or just a metric) on a smooth manifold is a choice of inner product for each tangent space of the manifold. A Riemannian...

In mathematics, a hyperbolic metric space is a metric space satisfying certain metric relations (depending quantitatively on a nonnegative real number...

topology, a Polish space is a separable completely metrizable topological space; that is, a space homeomorphic to a complete metric space that has a countable...

{\displaystyle X} is a discrete uniform space if it is equipped with its discrete uniformity. the discrete metric ρ {\displaystyle \rho } on X {\displaystyle...

Minkowski metric. Minkowski space is, in particular, not a metric space and not a Riemannian manifold with a Riemannian metric. However, Minkowski space contains...

pseudometric space is a generalization of a metric space in which the distance between two distinct points can be zero. Pseudometric spaces were introduced...

metric (FLRW), where it corresponds to an increase in the scale of the spatial part of the universe's spacetime metric tensor (which governs...

mathematics, metric may refer to one of two related, but distinct concepts: A function which measures distance between two points in a metric space A metric tensor...

Kolmogorov quotient is the one-point space. A first-countable, separable Hausdorff space (in particular, a separable metric space) has at most the continuum cardinality...

In the mathematical study of metric spaces, one can consider the arclength of paths in the space. If two points are at a given distance from each other...

theory, Met is a category that has metric spaces as its objects and metric maps (continuous functions between metric spaces that do not increase any pairwise...

a topological vector space. If this metric space is complete then the normed space is a Banach space. Every normed vector space can be "uniquely extended"...

analogue of an n-sphere (with its canonical Riemannian metric). The main application of de Sitter space is its use in general relativity, where it serves as...

In mathematics, a dilation is a function f {\displaystyle f} from a metric space M {\displaystyle M} into itself that satisfies the identity d ( f ( x...

usually agree in a metric space, but may not be equivalent in other topological spaces. One such generalization is that a topological space is sequentially...

mathematics, a metrizable space is a topological space that is homeomorphic to a metric space. That is, a topological space ( X , τ ) {\displaystyle (X...

space allows defining distances and angles there. More precisely, a metric tensor at a point p of M is a bilinear form defined on the tangent space at...

of topological spaces include Euclidean spaces, metric spaces and manifolds. Although very general, the concept of topological spaces is fundamental,...

These definitions coincide for subsets of a complete metric space, but not in general. A metric space ( M , d ) {\displaystyle (M,d)} is totally bounded...

product space Kolmogorov space Lp-space Lens space Liouville space Locally finite space Loop space Lorentz space Mapping space Measure space Metric space Minkowski...

analysis, a Banach space (pronounced [ˈbanax]) is a complete normed vector space. Thus, a Banach space is a vector space with a metric that allows the computation...

mathematics, the concept of distance has been generalized to abstract metric spaces, and other distances than Euclidean have been studied. In some applications...

detailed expositions of the definitions given below. Connection Curvature Metric space Riemannian manifold See also: Glossary of general topology Glossary of...

completely metrizable space (metrically topologically complete space) is a topological space (X, T) for which there exists at least one metric d on X such that...

mathematics, specifically in category theory, a generalized metric space is a metric space but without the symmetry property and some other properties...

called a semi-Riemannian manifold, is a differentiable manifold with a metric tensor that is everywhere nondegenerate. This is a generalization of a Riemannian...

or Kantorovich–Rubinstein metric is a distance function defined between probability distributions on a given metric space M {\displaystyle M} . It is...

Hausdorff distance, or Hausdorff metric, also called Pompeiu–Hausdorff distance, measures how far two subsets of a metric space are from each other. It turns...